题目内容
已知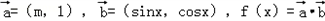 且满足
且满足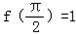 .
.
(1)求函数y=f(x)的解析式及最小正周期;
(2)在锐角三角形ABC中,若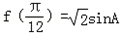 ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长.
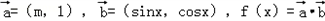 且满足
且满足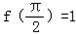 .
.(1)求函数y=f(x)的解析式及最小正周期;
(2)在锐角三角形ABC中,若
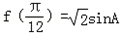 ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长.解:(1)∵ =(m,1),
=(m,1),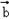 =(sinx,cosx)且f(x)=
=(sinx,cosx)且f(x)=
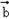 ,
,
∴f(x)=msinx+cosx,又f(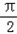 )=1,
)=1,
∴msin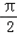 +cos
+cos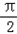 =1,
=1,
∴m=1,
∴f(x)=sinx+cosx=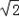 sin(x+
sin(x+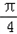 ),
),
∴函数f(x)的最小正周期T=2π;
(2)∵f(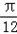 )=
)=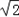 sinA,
sinA,
∴f(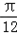 )=
)=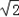 sin
sin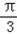 =
=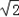 sinA,
sinA,
∴sinA=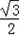 ,
,
∵A是锐角三角形ABC的内角,
∴A=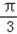 ,又AB=2,AC=3,
,又AB=2,AC=3,
∴由余弦定理得:BC2=AC2+AB2﹣2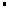 AB
AB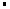 AC
AC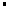 cosA=32+22﹣2×2×3×
cosA=32+22﹣2×2×3× =7,
=7,
∴BC=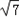 .
.
 =(m,1),
=(m,1),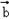 =(sinx,cosx)且f(x)=
=(sinx,cosx)且f(x)=
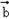 ,
,∴f(x)=msinx+cosx,又f(
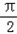 )=1,
)=1,∴msin
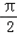 +cos
+cos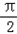 =1,
=1,∴m=1,
∴f(x)=sinx+cosx=
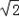 sin(x+
sin(x+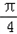 ),
),∴函数f(x)的最小正周期T=2π;
(2)∵f(
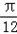 )=
)=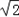 sinA,
sinA,∴f(
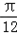 )=
)=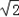 sin
sin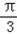 =
=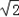 sinA,
sinA,∴sinA=
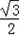 ,
,∵A是锐角三角形ABC的内角,
∴A=
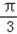 ,又AB=2,AC=3,
,又AB=2,AC=3,∴由余弦定理得:BC2=AC2+AB2﹣2
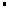 AB
AB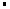 AC
AC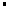 cosA=32+22﹣2×2×3×
cosA=32+22﹣2×2×3× =7,
=7,∴BC=
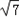 .
.
练习册系列答案
相关题目
 且满足
且满足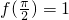 .
. ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长. 且满足
且满足 .
. ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长. 且满足
且满足 .
. ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长. 且满足
且满足 .
. ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长. 且满足
且满足 .
. ,且AB=2,AC=3,求BC的长.
,且AB=2,AC=3,求BC的长.