题目内容
在xOy平面上有一系列的点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)…对于正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的⊙Pn与x轴相切,且⊙Pn与⊙Pn+1又彼此外切,若x1=1,且xn+1<xn.
(1)求证:数列{
}是等差数列;
(2)设⊙Pn的面积为Sn,Tn=
+
+
+…+
,求证:Tn<
.
(1)求证:数列{
| 1 |
| xn |
(2)设⊙Pn的面积为Sn,Tn=
| S1 |
| S2 |
| S3 |
| Sn |
3
| ||
| 2 |
(1)证明:∵圆Pn与P(n+1)相切,且P(n+1)与x轴相切,
所以,Rn=Yn,R(n+1)=Y(n+1),且两圆心间的距离就等于两半径之和,即
=Yn+Y(n+1)
整理就可以得到,
-
=2
故数列{
}是等差数列
(2)S1=π(x1)4S2=π(x2)4…Sn=π(xn)4
约去
证明(x1)2+(x2)2+…(xn)2<
即可
由(1)知(x1)2+(x2)2+…(xn)2
=1+(
)2+(
)2+…(
)2
因为1+(
)2+(
)2+(
)2+…(
)2
=[1+(
)2+(
)2+…(
)2]+
[1+(
)2+(
)2+(
)2+…(
)2]
即1+(
)2+(
)2+…(
)2=
1+(
)2+(
)2+(
)2+…(
)2
又因为 1+[(
)2+(
)2+(
)2+(
)2+(
)2+(
)2]+(
)2+…
<1+[(
)2+(
)2+(
)2+(
)2+(
)2+(
)2+8(
)2+…
=1+
+
+
…=2
即就是1+(
)2+(
)2+(
)2+…(
)2<2
所以 1+(
)2+(
)2+…(
)<
×2=
即1+(
)2+(
)2+…(
)<
所以
+
+
+…+
<
即Tn<
所以,Rn=Yn,R(n+1)=Y(n+1),且两圆心间的距离就等于两半径之和,即
| (xn-xn+1)2+(yn-yn+1)2 |
整理就可以得到,
| 1 |
| xn+1 |
| 1 |
| xn |
故数列{
| 1 |
| xn |
(2)S1=π(x1)4S2=π(x2)4…Sn=π(xn)4
约去
| π |
| 3 |
| 2 |
由(1)知(x1)2+(x2)2+…(xn)2
=1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
因为1+(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
=[1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
即1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
又因为 1+[(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 8 |
<1+[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
=1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
即就是1+(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
所以 1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 4 |
| 3 |
| 2 |
即1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 2 |
所以
| S1 |
| S2 |
| S3 |
| Sn |
3
| ||
| 2 |
即Tn<
3
| ||
| 2 |

练习册系列答案
相关题目
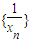 是等差数列;
是等差数列;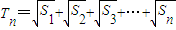 ,求证:
,求证: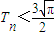 .
. =( )
=( )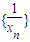 是等差数列;
是等差数列; ,求证:
,求证: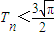 .
.