题目内容
若二次函数f(x)＝ax2＋bx＋c (a≠0)满足f(x＋1)－f(x)＝2x，且f(0)＝1.
(1)求f(x)的解析式；
(2)若在区间[－1,1]上，不等式f(x)>2x＋m恒成立，求实数m的取值范围．
因此，f(x)＝x2－x＋1.
(2)f(x)>2x＋m等价于x2－x＋1>2x＋m，即x2－3x＋1－m>0，要使此不等式在[－1,1]上恒成立，只需使函数g(x)＝x2－3x＋1－m在[－1,1]上的最小值大于0即可．
∵g(x)＝x2－3x＋1－m在[－1,1]上单调递减，
∴g(x)min＝g(1)＝－m－1，
由－m－1>0，得m<－1.
因此满足条件的实数m的取值范围是(－∞，－1)．
练习册系列答案
相关题目
等于 ( )
B、
C、
D、
为圆
上的两个点，
为
延长线上一点，
为圆
为切点. 若
，
，则
______；
______．
x，若f(x0)＝－9，则x0的值为( )
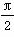)的部分图象如图所示，则( )
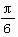B．ω＝1，φ＝－
，－
，
，…的一个通项公式是( )
B．an＝(－1)n·
D．an＝(－1)n·
D．
l2