Question

.将高一（6）班52名学生分成A，B两组参加学校组织的义务植树活动，A组种植150棵大叶榕树苗，B组种植200棵红枫树苗．假定A，B两组同时开始种植．每名学生种植一棵大叶榕树苗用时小时，种植一棵枫树苗用时小时．完成这次植树任务需要最短时间为

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

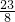
C
分析：设出分到A，B两组的人数，求出每组完成植树任务所用时间，当两组时间相等时用时间最短，列式求解得到的x为非整数解，说明两组学生不可能同时完成，取离x的值最近的两个整数值，分别代入两组学生的用时列式中，每一种情况的用时多的一组的时间为完成这次植树任务的用时，然后比较x取两个不同整数时的用时，取小者．
解答：设A组有x人，则B组有（52-x）人．
当两组同时完成植树任务时用时最短，据此列得方程为：
，即，
（0.4X150）/x=（0.5X200）/（52-x）
解得：x=19.5．
但是人不能是半人参加的，所以x取19或20．
把x依次带入19和20，
当x=19时，=，=．
因为，所以用时为；
当x=20时，=，=．
因为，所以用时为．
而．
所以最终当x=20时，完成这次植树任务需要最短时间，最短时间为．
故选C．
点评：本题考查了函数模型的选择及应用，考查了分类讨论的数学思想方法，解答此题的关键是注意实际问题要有实际意义，体现了学生灵活处理问题和解决问题的能力，是中档题．