题目内容
设
、
、
是三个向量,以下命题中真命题的序号是
①若
•
=
•
,且
≠0,则
=
;
②若
•
=0,则
=0或
=0;
③若
、
、
互不共线,则(
•
)
=
(
•
);
④(3
+2
)•(3
-2
)=9|
|2-4|
|2.
| a |
| b |
| c |
④
④
.①若
| a |
| b |
| a |
| c |
| a |
| b |
| c |
②若
| a |
| b |
| a |
| b |
③若
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
④(3
| a |
| b |
| a |
| b |
| a |
| b |
分析:分别根据向量的概念和数量积的定义和运算性质判断.
解答:解:①由
•
=
•
,得
?(
-
)=0,所以无法得到
=
,所以①错误.
②当非零向量
、
垂直时,满足
•
=0,所以②错误.
③因为(
•
)
与
向量平行,
(
•
)与向量
平行,所以(
•
)
=
(
•
)不一定成立,所以③正确.
④(3
+2
)•(3
-2
)=9|
|2-4|
|2.所以④正确.
故答案为:④
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| b |
| c |
②当非零向量
| a |
| b |
| a |
| b |
③因为(
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
④(3
| a |
| b |
| a |
| b |
| a |
| b |
故答案为:④
点评:本题主要考查向量的数量积运算,要求熟练掌握数量积的定义和运行性质.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
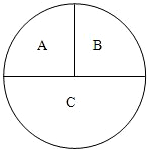 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.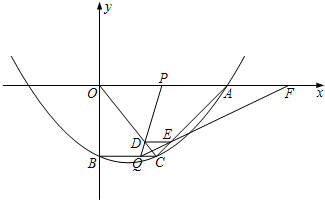 如图,在平面直角坐标系xoy中,抛物线y=
如图,在平面直角坐标系xoy中,抛物线y=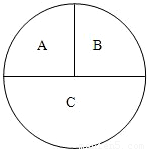 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.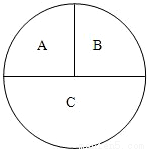 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.