题目内容
设 ,则( )
,则( )
A. | B. |
C. | D. |
D
解析试题分析:因为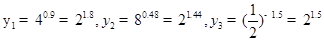
由于指数函数y=2x是递增函数,因此说那么大小关系必然为 ,选D.
,选D.
考点:本题主要是考查指数函数的值域的运用。
点评:解决该试题的关键是将不同底数的分数指数幂,化为同底的指数幂的形式,然后结合指数函数的 单调性得到结论。

练习册系列答案
相关题目
若函数 在
在 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 满足:x≥4,则
满足:x≥4,则 =
=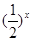 ;当x<4时
;当x<4时 =
=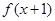 ,则
,则 =
=
A.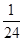 | B.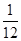 | C.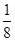 | D.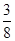 |
已知定义在 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 等于( )
等于( )
| A.4 | B.5 | C.6 | D.7 |
若 ,则
,则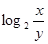 的值为( )
的值为( )
| A.0 | B.2 | C.-2 | D.0或2 |
2log510+log50.25=
| A.0 | B.1 | C.2 | D.4 |
若函数 的定义域为[0 , m],值域为
的定义域为[0 , m],值域为 ,则m的取值范围是( )
,则m的取值范围是( )
| A.(0 , 4] | B.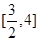 | C. | D. ) ) |
若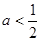 ,则化简
,则化简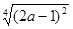 的结果是( )
的结果是( )
A.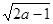 | B.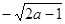 | C.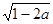 | D.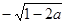 |
下列各式中成立的是( )
A. | B. |
C. | D. |