Question

已知一正方形的两个顶点为双曲线C的两个焦点，若另外两个顶点在双曲线C上，则双曲线C的离心率为（　　）

• A．

  5 +1

  2

• B．

  2 2

  3

• C．

  3

  +1
• D．

  2

  +1

Answer 1

分析：以焦点所在的边为x轴，以焦点所在的边的垂直平分线为y轴，建立平面直角坐标系，由题设条件求出a，c后就能求出双曲线的离心率．

解答：解：根据题意建立如上图所示的空直角坐标系，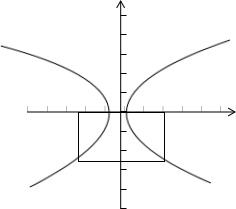
设正方形的边长为2，则双曲线的焦点坐标为（-1，0）和（1，0），且双曲线过点（1，-2）．
∵双曲线上的点（1，-2）到两个焦点（-1，0）和（1，0）的距离分别是2

2

和2，
∴a=

1

2

(2

2

-2)=

2

-1，
∵c=1，
∴e=

c

a

=

1

2 -1

=

2

+1．
答选D．

点评：本题考查双曲线的离心率的求法，是基础题．恰当地建立平面直角坐标系是正确解题的关键．