题目内容

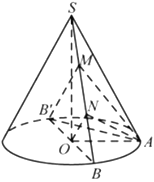
【题目】如图，在圆锥中，，是上的动点，是的直径，，是的两个三等分点，，记二面角，的平面角分别为，，若，则的最大值是（ ）

A.B.C.D.

【答案】B

【解析】

设底面圆的半径为,,以所在直线为轴,以垂直于所在直线为轴,以所在直线为轴建立空间直角坐标系,写出各个点的坐标.利用法向量求得二面角与夹角的余弦值.结合即可求得的取值范围,即可得的最大值.

设底面圆的半径为,,以所在直线为轴,以垂直于所在直线为轴,以所在直线为轴建立空间直角坐标系,如下图所示:

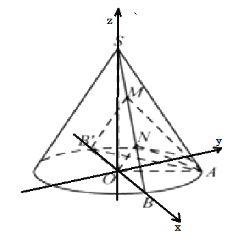
则由

可得,

,是的两个三等分点

则

所以

设平面的法向量为

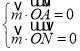则,代入可得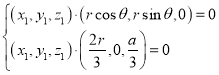

化简可得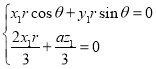

令,解得

所以

平面的法向量为

由图可知, 二面角的平面角为锐二面角,所以二面角的平面角满足

设二面角的法向量为

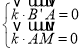则代入可得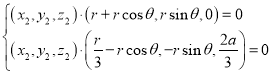

化简可得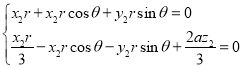

令,解得

所以

平面的法向量为

由图可知, 二面角的平面角为锐二面角,所以二面角的平面角满足

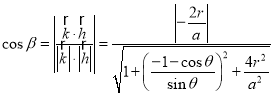
由二面角的范围可知

结合余弦函数的图像与性质可知

即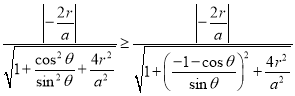

化简可得,且

所以

所以的最大值是

故选:B

练习册系列答案
相关题目

【题目】下列说法中正确的个数是_________.

（1）命题“若，则方程有实数根”的逆否命题为“若方程无实数根，则”.

（2）命题“，”的否定“，”.

（3）若为假命题，则，均为假命题.

（4）“”是“直线：与直线：平行”的充要条件.

【题目】如图，平面中两条直线和相交于点O，对于平面上任意一点M，若x，y分别是M到直线和的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：

①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；

②若pq=0，且p+q≠0，则“距离坐标”为（p，q）的点有且只有2个；

③若pq≠0则“距离坐标”为（p，q）的点有且只有4个．

上述命题中，正确命题的是______．（写出所有正确命题的序号）

【题目】如图，在菱形 中，，.

（1）若为的中点，则 ______

（2）点在线段上运动，则||的最小值为___________

【题目】如图，点F为椭圆C：(a＞b＞0)的左焦点，点A，B分别为椭圆C的右顶点和上顶点，点P(，)在椭圆C上，且满足OP∥AB．

（1）求椭圆C的方程；

（2）若过点F的直线l交椭圆C于D，E两点（点D位于x轴上方），直线AD和AE的斜率分别为和，且满足﹣＝﹣2，求直线l的方程．

【题目】已知椭圆经过点离心率为．

（Ⅰ）求椭圆的方程；

（Ⅱ）过点的直线交椭圆于两点，为椭圆的左焦点，若，求直线的方程．

【题目】已知椭圆：的离心率，且过焦点的最短弦长为3.

（1）求椭圆的标准方程；

（2）设分别是椭圆的左、右焦点，过点的直线与曲线交于不同的两点、，求的内切圆半径的最大值.

【题目】一个不透明的箱子中装有大小形状相同的5个小球，其中2个白球标号分别为，，3个红球标号分别为，，，现从箱子中随机地一次取出两个球.

（1）求取出的两个球都是白球的概率；

（2）求取出的两个球至少有一个是白球的概率.

【题目】已知定点，横坐标不小于的动点在轴上的射影为，若.

（1）求动点的轨迹的方程；

（2）若点不在直线上，并且直线与曲线相交于两个不同点.问是否存在常数使得当的值变化时，直线斜率之和是一个定值.若存在，求出的值；若不存在，请说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网