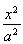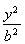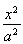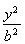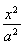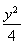题目内容
已知椭圆C1:
=1(a＞b＞0)的右焦点为F,上顶点为A,P为C1上任一点,MN是圆C2:x2+(y-3)2=1的一条直径.若与AF平行且在y轴上的截距为3-
的直线l恰好与圆C2相切.（1）求椭圆C1的离心率；
（2）若
·
的最大值为49，求椭圆C1的方程.
解:(1)直线l的方程为bx+cy-(3-2)c=0,
因为直线l与圆C2：x2+(y-3)2=1相切,所以d=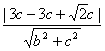=1.
可得2c2=a2,从而e=.
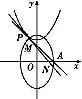
(2)设P(x,y),则·=(
+
)·(
+
)=
-
=x2+y2+6y-x12+y1(6-y1)=x2+y2+6y+8=-(y+3)2+2c2+17.
①当c≥3时,(
·
)max=17+2c2=49.
解得c=4,此时椭圆C1为
+
=1.
②当0＜c＜3时,(
·
)max=-(-c+3)2+17+2c2=49,解得c=5
-3,
但(5
-3)-3=
-6＞0,所以5
-3＞3,故c=5
-3舍去.
综上所述,椭圆C1的方程为
+
=1.
练习册系列答案
相关题目
=1，其左准线为l1，右准线为l2，一条以原点为顶点，l1为准线的抛物线C2交l2于A、B两点，则|AB|等于（ ）
=1，其左准线为l1，右准线为l2，一条以原点为顶点，l1为准线的抛物线C2交l2于A、B两点，则|AB|等于( )
