题目内容
(12分)已知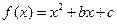 为偶函数,曲线
为偶函数,曲线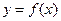 过点
过点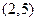 ,
,
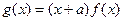 .
.
(1)若曲线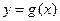 存在斜率为0的切线,求实数
存在斜率为0的切线,求实数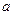 的取值范围;
的取值范围;
(2)若当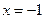 时函数
时函数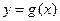 取得极值,确定
取得极值,确定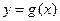 的单调区间.
的单调区间.
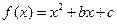 为偶函数,曲线
为偶函数,曲线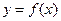 过点
过点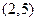 ,
,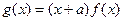 .
.(1)若曲线
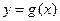 存在斜率为0的切线,求实数
存在斜率为0的切线,求实数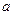 的取值范围;
的取值范围;(2)若当
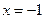 时函数
时函数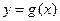 取得极值,确定
取得极值,确定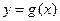 的单调区间.
的单调区间.解: (Ⅰ)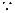
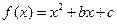 为偶函数,故
为偶函数,故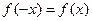 即有
即有
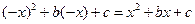 解得
解得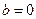
又曲线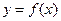 过点
过点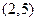 ,得
,得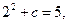 有
有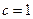
因为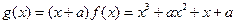 从而
从而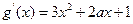 ,
,
又因为曲线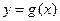 有斜率为0的切线,
有斜率为0的切线,
故有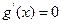 有实数解.即
有实数解.即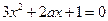 有实数解.
有实数解.
此时有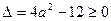 解得
解得 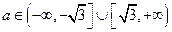
所以实数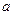 的取值范围:
的取值范围: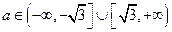
(Ⅱ)因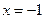 时函数
时函数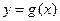 取得极值,
取得极值,
故有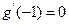 即
即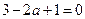 ,解得
,解得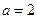
又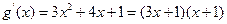
令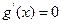 ,得
,得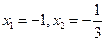
当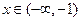 时,
时, 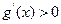 ,故
,故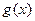 在
在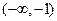 上为增函数
上为增函数
当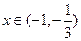 时,
时, 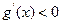 ,故
,故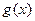 在
在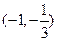 上为减函数
上为减函数
当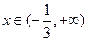 时,
时, 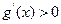 ,故
,故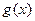 在
在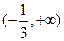 上为增函数
上为增函数
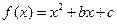 为偶函数,故
为偶函数,故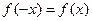 即有
即有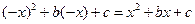 解得
解得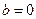
又曲线
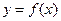 过点
过点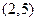 ,得
,得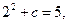 有
有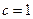
因为
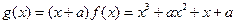 从而
从而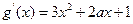 ,
,又因为曲线
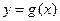 有斜率为0的切线,
有斜率为0的切线,故有
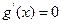 有实数解.即
有实数解.即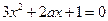 有实数解.
有实数解.此时有
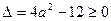 解得
解得 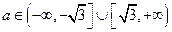
所以实数
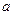 的取值范围:
的取值范围: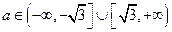
(Ⅱ)因
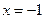 时函数
时函数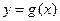 取得极值,
取得极值,故有
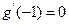 即
即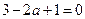 ,解得
,解得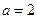
又
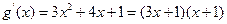
令
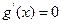 ,得
,得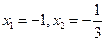
当
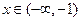 时,
时, 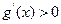 ,故
,故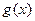 在
在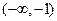 上为增函数
上为增函数当
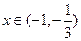 时,
时, 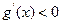 ,故
,故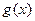 在
在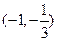 上为减函数
上为减函数当
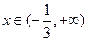 时,
时, 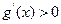 ,故
,故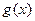 在
在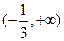 上为增函数
上为增函数略

练习册系列答案
相关题目
 。已知2010年生产饮料的设备折旧
。已知2010年生产饮料的设备折旧 ,维修等固定费用为3 万元,每生产1万件
,维修等固定费用为3 万元,每生产1万件 成本—促销费,生产成本=固定费用+生产费用)
成本—促销费,生产成本=固定费用+生产费用)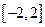 上的奇函数
上的奇函数 满足当
满足当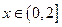 时,
时,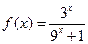 .
.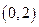 上的单调性,并给予证明;
上的单调性,并给予证明;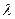 为何值时,关于方程
为何值时,关于方程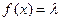 在
在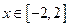 上有实数解?
上有实数解?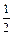 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?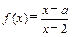 ,
, 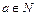 ,且函数
,且函数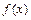 在区间(2,+∞)上是减函数,则
在区间(2,+∞)上是减函数,则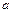
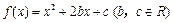 ,且
,且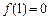 .
.
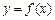 与x轴的两个交点
与x轴的两个交点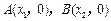 之间的距离为2,求b的值;
之间的距离为2,求b的值; 方程
方程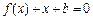 的两个实数根分别在区间
的两个实数根分别在区间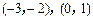 内,求b的取值范
内,求b的取值范 围.
围.