Question

已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=2^x-1．
（Ⅰ）求f（3）+f（-1）；
（Ⅱ）求f（x）的解析式；
（Ⅲ）若x∈A，f（x）∈[-7，3]，求区间A．

Answer 1

分析：（Ⅰ）根据奇函数的性质代入已知式子可求；
（Ⅱ）设x＜0，则-x＞0，易求f（-x），根据奇函数性质可得f（x）与f（-x）的关系；
（Ⅲ）作出f（x）的图象，由图象可知f（x）单调递增，由f（x）=-7及f（x）=3可求得相应的x值，结合图象可求得A；

解答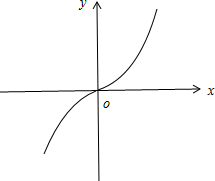：解：（Ⅰ）∵f（x）是奇函数，
∴f（3）+f（-1）=f（3）-f（1）=2³-1-2+1=6；
（Ⅱ）设x＜0，则-x＞0，∴f（-x）=2^-x-1，
∵f（x）为奇函数，∴f（x）=-f（-x）=-2^-x+1，
∴f(x)=

2x-1，x≥0 -2-x+1， x＜0

；
（Ⅲ）作出函数f（x）的图象，如图所示：
根据函数图象可得f（x）在R上单调递增，
当x＜0时，-7≤-2^-x+1＜0，解得-3≤x＜0；
当x≥0时，0≤2^x-1≤3，解得0≤x≤2；
∴区间A为[-3，2]．

点评：本题考查函数的奇偶性及其应用，考查指数不等式的求解，考查数形结合思想，考查学生解决问题的能力．