题目内容
(本题满分12分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入资金x(万元)的关系有经验公式:P= x,Q=
x,Q=
 .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
【答案】
为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,获得最高利润1.05万元.
【解析】本题考查了二次根式在实际问题中的运用.关键是根据题意列方程,两边平方去根号转化为关于x的一元二次方程,利用判别式求解.
根据3万元资金投入经营甲、乙两种商品,设投入甲x万元,则投入乙(3-x)万元,根据总利润=甲的利润+乙的利润,列方程并平方整理为关于x的一元二次方程,由△≥0,求s的最大值,并求出此时x的值.
解:设对甲种商品投资x万元,获总利润为y万元,则对乙种商品的投资为(3-x)万元,于是y= x+
x+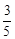
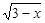 (0≤x≤3).
(0≤x≤3).
令t=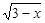 (0≤t≤
(0≤t≤ ),则x=3-t2,
),则x=3-t2,
∴y= (3-t2)+
(3-t2)+
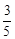 t=
t= (3+3t-t2)
=-
(3+3t-t2)
=- (t-
(t-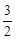 )2+
)2+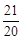 ,t∈[0,
,t∈[0, ].
].
∴当t=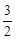 时,ymax=
时,ymax=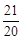 =1.05(万元); 由t=
=1.05(万元); 由t=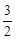 可求得x=0.75(万元), 3-x=2.25(万元),
可求得x=0.75(万元), 3-x=2.25(万元),
∴为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,获得最高利润1.05万元.

练习册系列答案
相关题目
 万元和
万元和 万元,它们与投入资金万元的关系为:
万元,它们与投入资金万元的关系为: 今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少?
今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少? =
= 。
。 有零点的概率;
有零点的概率;