题目内容

A为椭圆上任意一点，B为圆(x-1)2+y2=1上任意一点，求|AB|的最大值和最小值.

解析：化普通方程为参数方程,再求出圆心坐标,利用两点间距离公式转化为三角函数求值域问题来解决.

解：化普通方程为参数方程(θ为参数),圆心坐标为C(1,0),再根据平面内两点之间的距离公式可得

|AC|=

=

=,

所以,当cosθ=时,|AC|取最小值为；当cosθ=-1时,|AC|取最大值为6.

所以,当cosθ=516时,|AB|取最小值为+1；

当cosθ=-1时,|AB|取最大值为6+1=7.

练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
1
2
，F1、F2分别为椭圆C的左、右焦点，若椭圆C的焦距为2．
（1）求椭圆C的方程；
（2）设M为椭圆上任意一点，以M为圆心，MF1为半径作圆M，当圆M与直线l：x=
a2
c
有公共点时，求△MF1F2面积的最大值．
F1，F2为椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)左、右焦点，A为椭圆上任意一点，过焦点F2向∠F1AF2的外角平分线作垂线，垂足为D，则点D的轨迹方程是x2+y2=a2．类比可得：F1，F2为双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)左、右焦点，A为双曲线上任意一点，过焦点F2向∠F1AF2的
内角
内角
平分线作垂线，垂足为D，则点D的轨迹方程是
x2+y2=a2
x2+y2=a2
．
A为椭圆上任意一点，B为圆(x-1)2+y2=1上任意一点，求|AB|的最大值和最小值.

F1，F2为椭圆左、右焦点，A为椭圆上任意一点，过焦点F2向∠F1AF2的外角平分线作垂线，垂足为D，则点D的轨迹方程是x2+y2=a2．类比可得：F1，F2为双曲线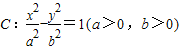左、右焦点，A为双曲线上任意一点，过焦点F2向∠F1AF2的    平分线作垂线，垂足为D，则点D的轨迹方程是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网