题目内容
已知tan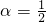
，tan（α-β）=-
，则tan（β-2α）=
- A.-
- B.
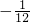
- C.
- D.
B
分析：先把所求的式子中的角β-2α变为（β-α）-α，然后利用两角差的正切函数公式化简后，把已知的tanα和tan（β-α）的值代入即可求出值．
解答：解；∵tan，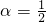
∴tan（β-2α）=-tan（2α-β）=-tan[（α-β）+α]
=-
=-
=-
．
故选B．
点评：此题考查学生灵活运用两角差的正切函数公式化简求值，是一道基础题．学生做题时应注意角度的灵活变换．
分析：先把所求的式子中的角β-2α变为（β-α）-α，然后利用两角差的正切函数公式化简后，把已知的tanα和tan（β-α）的值代入即可求出值．
解答：解；∵tan
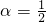，∴tan（β-2α）=-tan（2α-β）=-tan[（α-β）+α]
=-
=-=-．故选B．
点评：此题考查学生灵活运用两角差的正切函数公式化简求值，是一道基础题．学生做题时应注意角度的灵活变换．
练习册系列答案
名校课堂系列答案
相关题目
已知命题（1）?α∈R，使sinαcosα=1成立；（2）?α∈R，使tan（α+β）=tanα+tanβ成立；（3）?α∈R，都有tan(α+β)=
成立．其中正确命题的个数是（ ）
| tanα+tanβ |
| 1-tanαtanβ |
| A、3 | B、2 | C、1 | D、0 |
已知tanα，tanβ是方程x2+3
x+4=0的两根，且α，β∈(-
，
)，则α+β=（ ）
| 3 |
| π |
| 2 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|