题目内容
 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且满足BD•BE=BA•BF.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且满足BD•BE=BA•BF.求证:
(1)EF⊥FB;
(2)∠DFB+∠DBC=90°.
分析:(1)利用BD•BE=BA•BF,可得
=
,从而可知△ADB∽△EFB,可得∠EFB=∠ADB,利用AB是⊙O的直径,即可得到结论;
(2)先证明E、F、A、D四点共圆,从而可得∠DFB=∠AEB,利用AB是⊙O的直径,可证结论成立.
| BD |
| BA |
| BF |
| BE |
(2)先证明E、F、A、D四点共圆,从而可得∠DFB=∠AEB,利用AB是⊙O的直径,可证结论成立.
解答: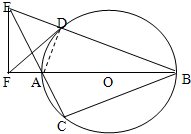 (1)证明:连接AD,则∵AB是⊙O的直径,∴∠ADB=90°
(1)证明:连接AD,则∵AB是⊙O的直径,∴∠ADB=90°
在△ADB和△EFB中,∵BD•BE=BA•BF,∴
=
…..(2分)
又∠DBA=∠EBF,∴△ADB∽△EFB…..(4分)
则∠EFB=∠ADB=90°,∴EF⊥FB…..(5分)
(2)在△ADB中,∠ADB=∠ADE=90°
又∠EFB=90°∴E、F、A、D四点共圆; …(7分)
∴∠DFB=∠AEB…..(9分)
又AB是⊙O的直径,则∠ACB=90°,
∴∠DFB+∠DBC=∠AEB+∠DBC=90°…(10分)
 (1)证明:连接AD,则∵AB是⊙O的直径,∴∠ADB=90°
(1)证明:连接AD,则∵AB是⊙O的直径,∴∠ADB=90°在△ADB和△EFB中,∵BD•BE=BA•BF,∴
| BD |
| BA |
| BF |
| BE |
又∠DBA=∠EBF,∴△ADB∽△EFB…..(4分)
则∠EFB=∠ADB=90°,∴EF⊥FB…..(5分)
(2)在△ADB中,∠ADB=∠ADE=90°
又∠EFB=90°∴E、F、A、D四点共圆; …(7分)
∴∠DFB=∠AEB…..(9分)
又AB是⊙O的直径,则∠ACB=90°,
∴∠DFB+∠DBC=∠AEB+∠DBC=90°…(10分)
点评:本题考查三角形的相似,考查四点共圆,掌握三角形相似的判定方法是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






 面体中有
面体中有 个面是直角三角形,则称这个
个面是直角三角形,则称这个 .那么四面体
.那么四面体 的直度为多少?说明理由;
的直度为多少?说明理由; (2)在四面体
(2)在四面体 ,设
,设 .若动点
.若动点 在四面体
在四面体 .设
.设 为动点
为动点 的函数,求
的函数,求 的正切值.
的正切值.