题目内容
设奇函数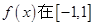 上是增函数,且
上是增函数,且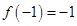 ,若函数
,若函数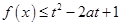 对所有的
对所有的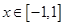 都成立,则当
都成立,则当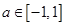 时t的取值范围是 ( )
时t的取值范围是 ( )
A.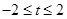 B.
B.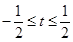
C.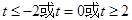 D.
D.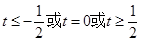
【答案】
C
【解析】
试题分析:由题意得:函数 上的最大值为
上的最大值为 ,则要使不等式
,则要使不等式
 成立,只需
成立,只需 ,即
,即 ,当
,当 时,
时, ,则由
,则由 得:
得: ;当
;当 时,
时, 成立;当
成立;当 时,
时, ,则由
,则由 得:
得: ,综上
,综上 。故选C。
。故选C。
考点:函数的性质
点评:不等式的问题,常需要结合函数的单调性来求解。像本题解不等式 ,只要确定函数
,只要确定函数 的最大值,然后让
的最大值,然后让 大于或等于最大值即可。
大于或等于最大值即可。

练习册系列答案
相关题目
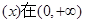 上是增函数,且
上是增函数,且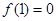 ,则不等式
,则不等式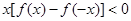 的解集为( )
的解集为( )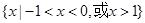 B.
B.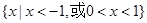
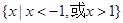 D.
D.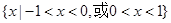
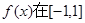 上是增函数,且
上是增函数,且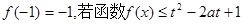 对所有的
对所有的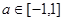 ,
,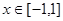 都成立,则t的取值范围是________________.
都成立,则t的取值范围是________________.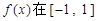 上是增函数,且
上是增函数,且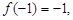 若函数
若函数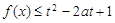 对所有的
对所有的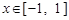 都成立,当
都成立,当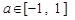 时,则t的取值范围是 ( )
时,则t的取值范围是 ( )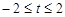 B.
B.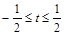
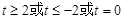 D.
D.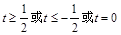
 上是增函数,且
上是增函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B.
 D.
D.