Question

【题目】△ABC中内角A、B、C的对边分别为a、b、c，且2acosC=2b﹣c．
（Ⅰ）求角A的大小；
（Ⅱ）如果a=1，求b+c的取值范围．

Answer 1

【答案】解：（Ⅰ）2acosC=2b﹣c，由正弦定理可得：sinAcosC+ sinC=sinB， sinB=sin（A+C）=sinAcosC+cosAsinC．∴ sinC=cosAsinC，∵sinC≠0，
∴cosA= ，
角A的大小为： ；
（Ⅱ）由正弦定理可得：b= ， ，
∴b+c= = = ，
∵ ∴ ，
∴ ∈ ，
∴ ，
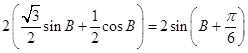∴b+c的取值范围：（1，2]．
【解析】（Ⅰ）利用正弦定理以及两角和与差的三角函数，化简方程，即可求角A的余弦值，得到A的值；（Ⅱ）利用正弦定理区别b，c的值，b+c为B的正弦函数，通过三角函数值域，求出b+c的取值范围．
【考点精析】根据题目的已知条件，利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:；余弦定理:;;．