题目内容
14.一个圆的圆心在抛物线y2=16x上,且该圆经过抛物线的顶点和焦点,若圆心在第一象限,则该圆的标准方程是(x-2)2+(y-4$\sqrt{2}$)2=36.分析 由题意可得圆心在线段OF的中垂线x=2上,代入抛物线方程可得圆心坐标,半径r,进而得到圆的方程.
解答 解:由题知,F(4,0),圆心在线段OF的中垂线x=2上,
由$\left\{\begin{array}{l}{{y}^{2}=16x}\\{x=2}\end{array}\right.$,圆心在第一象限,解得x=2,y=4$\sqrt{2}$,
则圆心C为(2,4$\sqrt{2}$),半径r=|CF|=6,
所以圆的方程是:(x-2)2+(y-4$\sqrt{2}$)2=36.
故答案为:(x-2)2+(y-4$\sqrt{2}$)2=36.
点评 本题考查圆的方程的求法,抛物线的定义和方程、性质的运用,属于中档题.

练习册系列答案
相关题目
5.设a,b是两条不同的直线,α,β为两个不重合的平面,下列命题中的真命题的是( )
| A. | 若a,b与α所成的角相等,则a∥b | B. | 若a∥α,b∥β,α∥β,则a∥b | ||
| C. | 若a?α,b?β,α⊥β,则 a⊥b | D. | 若a⊥α,b⊥β,α∥β,则a∥b |
6.已知函数f(x)的导数f'(x),f(x)不是常数函数,且(x+1)f(x)+xf'(x)≥0,对x∈[0,+∞)恒成立,则下列不等式一定成立的是( )
| A. | ef(1)<f(2) | B. | f(1)<0 | C. | ef(e)<2f(2) | D. | f(1)<2ef(2) |
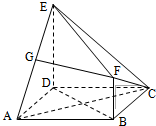 在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED.
在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED. 如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,