题目内容
已知数列{an}是各项均为正数的等比数列,且a1+a2=2(
+
),a3+a4=32(
+
).
(1)求数列{an}的通项公式;
(2)设bn=
•log2an,求数列{bn}的前n项和Sn.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
(1)求数列{an}的通项公式;
(2)设bn=
| a | 2 n |
分析:(1)由题意,化简已知可得a1a2=2,a3a4=32,两式相比可得公比,进而得首项,易得通项公式;
(2)结合(1)可得数列{bn}的通项公式,由错位相减法可求和.
(2)结合(1)可得数列{bn}的通项公式,由错位相减法可求和.
解答:解:(1)∵a1+a2=2(
+
)=2×
,
a3+a4=32(
+
)=32×
,
又因为数列{an}各项均为正数.
∴a1a2=2,a3a4=32,
∴q4=
=16,∴q=2
又a1a2=a1•a1q=2,∴a1=1
∴an=a1qn-1=2n-1
(2)由(1)可知an=2n-1,
∴bn=an2•log2an
∴bn=4n-1•(n-1)
∴Sn=0×40+41+2×42+3×43+…+(n-1)•4n-1 ①
4Sn=0×41+42+2×43+…+(n-2)4n-1+(n-1)•4n ②
①-②得:-3Sn=4+42+43+…+4n-1-(n-1)•4n
=
-(n-1)•4n
∴Sn=
•4n+
| 1 |
| a1 |
| 1 |
| a2 |
| a1+a2 |
| a1a2 |
a3+a4=32(
| 1 |
| a3 |
| 1 |
| a4 |
| a3+a4 |
| a3a4 |
又因为数列{an}各项均为正数.
∴a1a2=2,a3a4=32,
∴q4=
| a3a4 |
| a1a2 |
又a1a2=a1•a1q=2,∴a1=1
∴an=a1qn-1=2n-1
(2)由(1)可知an=2n-1,
∴bn=an2•log2an
∴bn=4n-1•(n-1)
∴Sn=0×40+41+2×42+3×43+…+(n-1)•4n-1 ①
4Sn=0×41+42+2×43+…+(n-2)4n-1+(n-1)•4n ②
①-②得:-3Sn=4+42+43+…+4n-1-(n-1)•4n
=
| 4(1-4n-1) |
| 1-4 |
∴Sn=
| (3n-4) |
| 9 |
| 4 |
| 9 |
点评:本题考查等差数列和等比数列的综合应用,涉及错位相减法求和,属中档题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足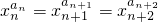 (n∈N*).
(n∈N*).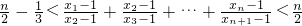 .
. (n∈N*).
(n∈N*). .
.
 (n∈N*).
(n∈N*). .
.