题目内容
在△ABC中,A,B,C的对边分别为a,b,c,向量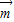 =(a,b),
=(a,b),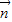 =(b,c).
=(b,c).(1)若向量
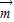
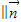 ,求满足
,求满足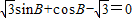 的角B的值;
的角B的值;(2)若

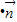 =2b2,且A-C=
=2b2,且A-C=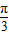 ,求cosB的值.
,求cosB的值.
【答案】分析:(1)由两个向量平行的坐标表示求出a、b、c的关系,借助于余弦定理求出角B的取值范围,最后根据等式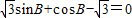 求出角B的值;
求出角B的值;
(2)把两个向量的坐标代入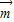
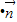 =2b2,找出a、b、c的关系,然后运用正弦定理转化为角的关系,再借助于三角形内角和定理把角都转化为角B,先求出
=2b2,找出a、b、c的关系,然后运用正弦定理转化为角的关系,再借助于三角形内角和定理把角都转化为角B,先求出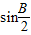 后,运用二倍角的余弦可求cosB.
后,运用二倍角的余弦可求cosB.
解答:解:(1)∵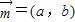 ,
,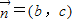 ,
,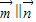 ,∴b2=ac,
,∴b2=ac,
∴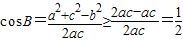 ,当且仅当a=c时取等号,∵0<B<π,∴
,当且仅当a=c时取等号,∵0<B<π,∴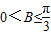 .
.
由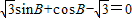 得:
得: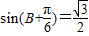 ,
,
∵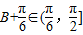 ,
,
∴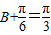 ,
,
∴B=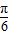 .
.
(2)在△ABC中,∵A-C=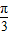 ,A+C=π-B,∴
,A+C=π-B,∴ ,
,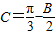 ,
,
∵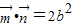 ,∴a+c=2b,∴sinA+sinC=2sinB,
,∴a+c=2b,∴sinA+sinC=2sinB,
∴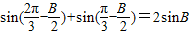 ,展开化简,得:
,展开化简,得: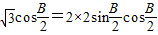 ,
,
∵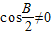 ,∴sin
,∴sin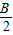 =
=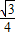 ,
,
∴cosB=1-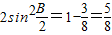 .
.
点评:本题考查了平面向量的数量积的坐标表示、模及夹角,考查了平面向量共线的条件,考查了转化思想,解答此题的关键是借助于正弦和余弦定理进行边和角的互化,是中等难度问题.
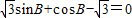 求出角B的值;
求出角B的值;(2)把两个向量的坐标代入
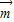
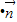 =2b2,找出a、b、c的关系,然后运用正弦定理转化为角的关系,再借助于三角形内角和定理把角都转化为角B,先求出
=2b2,找出a、b、c的关系,然后运用正弦定理转化为角的关系,再借助于三角形内角和定理把角都转化为角B,先求出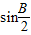 后,运用二倍角的余弦可求cosB.
后,运用二倍角的余弦可求cosB.解答:解:(1)∵
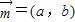 ,
,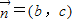 ,
,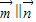 ,∴b2=ac,
,∴b2=ac,∴
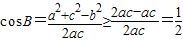 ,当且仅当a=c时取等号,∵0<B<π,∴
,当且仅当a=c时取等号,∵0<B<π,∴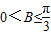 .
.由
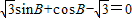 得:
得: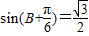 ,
,∵
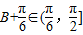 ,
,∴
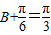 ,
,∴B=
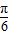 .
.(2)在△ABC中,∵A-C=
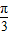 ,A+C=π-B,∴
,A+C=π-B,∴ ,
,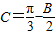 ,
,∵
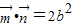 ,∴a+c=2b,∴sinA+sinC=2sinB,
,∴a+c=2b,∴sinA+sinC=2sinB,∴
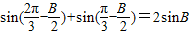 ,展开化简,得:
,展开化简,得: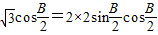 ,
,∵
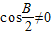 ,∴sin
,∴sin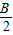 =
=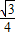 ,
,∴cosB=1-
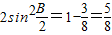 .
.点评:本题考查了平面向量的数量积的坐标表示、模及夹角,考查了平面向量共线的条件,考查了转化思想,解答此题的关键是借助于正弦和余弦定理进行边和角的互化,是中等难度问题.

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|