题目内容
已知二次函数f(x)=x2+x,若不等式f(-x)+f(x)≤2|x|的解集为C,
(Ⅰ)求集合C;
(Ⅱ)若方程f(ax)-ax+1=5(a>0,a≠1)在C上有解,求实数a的取值范围;
(Ⅲ)记f(x)在C上的值域为A,若 ,x∈[0,1]的值域为B,且
,x∈[0,1]的值域为B,且 ,求实数t的取值范围。
,求实数t的取值范围。
(Ⅰ)求集合C;
(Ⅱ)若方程f(ax)-ax+1=5(a>0,a≠1)在C上有解,求实数a的取值范围;
(Ⅲ)记f(x)在C上的值域为A,若
 ,x∈[0,1]的值域为B,且
,x∈[0,1]的值域为B,且 ,求实数t的取值范围。
,求实数t的取值范围。解:(Ⅰ)f(x)+f(-x)=2x2,
当x ≥0时,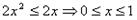 ;
;
当x<0时,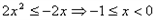 ;
;
∴集合C=[-1 ,1] 。
(Ⅱ)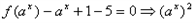
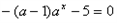 ,
,
令ax=u,
则方程为h(u)=u2-(a-1)u-5=0,h(0)=-5,
当a>1时,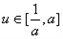 ,h(u)=0在
,h(u)=0在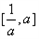 上有解,
上有解,
则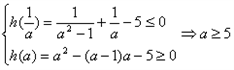 ;
;
当0<a<1时,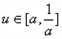 ,g(u)=0在
,g(u)=0在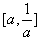 上有解,
上有解,
则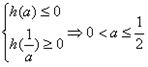 ;
;
∴当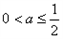 或a≥5时,方程在C上有解,且有唯一解。
或a≥5时,方程在C上有解,且有唯一解。
(Ⅲ)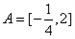 ,g′(x)=3x2-3t,
,g′(x)=3x2-3t,
①当t≤0时,g′(x)≥0,函数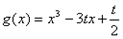 在x∈[0,1]单调递增,
在x∈[0,1]单调递增,
∴函数g(x)的值域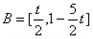 ,
,
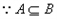 ,
,
∴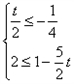 ,解得
,解得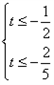 ,即
,即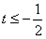 ;
;
②当t ≥1,g′(x )≤0 ,函数g(x)在区间[0,1] 单调递减,
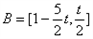 ,
,
∴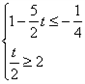 ,
,
又t≥1,
所以t≥4;
③当0<t<1时,令g′(x)=0得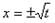 (舍去负值),
(舍去负值),
当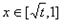 时,g′(x)>0;当
时,g′(x)>0;当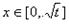 时,g′(x)<0,
时,g′(x)<0,
∴函数g(x)在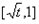 单调递增,在
单调递增,在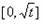 单调递减,g(x)在
单调递减,g(x)在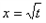 达到最小值;
达到最小值;
要使 ,则
,则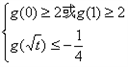
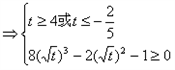 ,无解;
,无解;
综上所述:t的取值范围是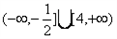 。
。
当x ≥0时,
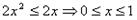 ;
;当x<0时,
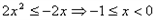 ;
;∴集合C=[-1 ,1] 。
(Ⅱ)
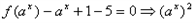
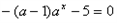 ,
,令ax=u,
则方程为h(u)=u2-(a-1)u-5=0,h(0)=-5,
当a>1时,
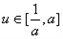 ,h(u)=0在
,h(u)=0在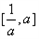 上有解,
上有解,则
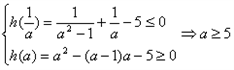 ;
;当0<a<1时,
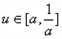 ,g(u)=0在
,g(u)=0在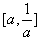 上有解,
上有解,则
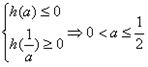 ;
;∴当
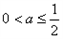 或a≥5时,方程在C上有解,且有唯一解。
或a≥5时,方程在C上有解,且有唯一解。(Ⅲ)
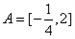 ,g′(x)=3x2-3t,
,g′(x)=3x2-3t,①当t≤0时,g′(x)≥0,函数
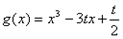 在x∈[0,1]单调递增,
在x∈[0,1]单调递增,∴函数g(x)的值域
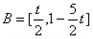 ,
, ,
,∴
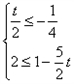 ,解得
,解得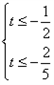 ,即
,即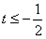 ;
;②当t ≥1,g′(x )≤0 ,函数g(x)在区间[0,1] 单调递减,
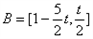 ,
,∴
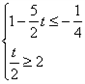 ,
,又t≥1,
所以t≥4;
③当0<t<1时,令g′(x)=0得
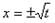 (舍去负值),
(舍去负值),当
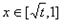 时,g′(x)>0;当
时,g′(x)>0;当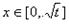 时,g′(x)<0,
时,g′(x)<0,∴函数g(x)在
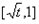 单调递增,在
单调递增,在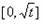 单调递减,g(x)在
单调递减,g(x)在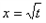 达到最小值;
达到最小值;要使
 ,则
,则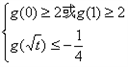
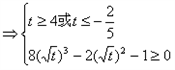 ,无解;
,无解;综上所述:t的取值范围是
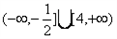 。
。
练习册系列答案
相关题目