题目内容
在正方体ABCD-A1B1C1D1中，P为棱BB1的中点，则在平面BCC1B1内过点P与直线AC成50°角的直线有
- A.0条
- B.1条
- C.2条
- D.无数条
C
分析：求出直线AC与平面BCC1B1内直线所成角的范围，结合已知条件，即可判断直线的条数．
解答：如图由题意可知，直线AC与平面BCC1B1内直线所成角的范围是[45°，90°]．
cos∠PCA=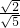
，∠PCA≠50°，所以在平面BCC1B1内过点P与直线AC成50°角的直线有2条．
故选C．
点评：本题是中档题，考查空间几何体的直线与直线的位置关系，注意角的判断是解题的关键，考查空间想象能力．
分析：求出直线AC与平面BCC1B1内直线所成角的范围，结合已知条件，即可判断直线的条数．
解答：如图由题意可知，直线AC与平面BCC1B1内直线所成角的范围是[45°，90°]．
cos∠PCA=
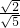，∠PCA≠50°，所以在平面BCC1B1内过点P与直线AC成50°角的直线有2条．故选C．
点评：本题是中档题，考查空间几何体的直线与直线的位置关系，注意角的判断是解题的关键，考查空间想象能力．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）