题目内容
设函数 ,
,
(1)求证:不论a为何实数f(x)总为增函数;
(2)确定a的值,使f(x)为奇函数及此时f(x)的值域.
 ,
,(1)求证:不论a为何实数f(x)总为增函数;
(2)确定a的值,使f(x)为奇函数及此时f(x)的值域.
解:(1)∵f(x)的定义域为R,设 x1<x2,则 =
= ,
,
∵x1<x2,
∴ ,
,
∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),
所以不论a为何实数f(x)总为增函数.
(2)∵f(x)为奇函数,
∴f(﹣x)=﹣f(x),即 ,
,
解得:a=1.
∴
∵2x+1>1,
∴ ,
,
∴
所以f(x)的值域为(﹣1,1).
 =
= ,
,∵x1<x2,
∴
 ,
,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),
所以不论a为何实数f(x)总为增函数.
(2)∵f(x)为奇函数,
∴f(﹣x)=﹣f(x),即
 ,
,解得:a=1.
∴

∵2x+1>1,
∴
 ,
,∴

所以f(x)的值域为(﹣1,1).

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
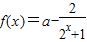 ,
,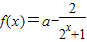 ,
,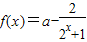 ,
,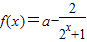 ,
,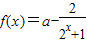 ,
,