题目内容
如图P是正方形ABCD的对角线BD上一点,PECF是矩形,用向量法证明: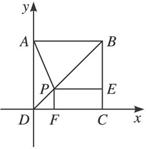
(1)PA=EF;(2)PA⊥EF.
证明:建立如上图所示的坐标系,设正方形的边长为1,|![]() |=λ,则A(0,1),P(
|=λ,则A(0,1),P(![]() λ,
λ,![]() λ),E(1,
λ),E(1,![]() λ),F(
λ),F(![]() λ,0),
λ,0),
∴![]() =(-
=(-![]() λ,1-
λ,1-![]() λ),
λ),![]() =(
=(![]() λ-1,-
λ-1,-![]() λ).
λ).
(1)∵|![]() |2=(-
|2=(-![]() λ)2+(1-
λ)2+(1-![]() λ)2=λ2-
λ)2=λ2-![]() +1,
+1,
|![]() |2=(
|2=(![]() λ-1)2+(-
λ-1)2+(-![]() λ)2=λ2-
λ)2=λ2-![]() +1,
+1,
∴|![]() |2=|
|2=|![]() |2,故PA=EF.
|2,故PA=EF.
(2)∵![]() ·
·![]() =(-
=(-![]() λ)(
λ)(![]() λ-1)+(1-
λ-1)+(1-![]() λ)·(-
λ)·(-![]() λ)=0,∴
λ)=0,∴![]() ⊥
⊥![]() ,即PA⊥EF.
,即PA⊥EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
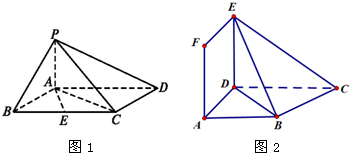
 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M,N分别是PA,BC的中点,且PD=AD=1.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M,N分别是PA,BC的中点,且PD=AD=1. 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
