题目内容
已知岛B、C分别在灯塔O的正西和正东方向且与灯塔O的距离都是2海里，岛A在岛B的正北
海里，海岸线（曲线PQ）上任一点到岛B、C的距离和是8海里，若岛B上无人，岛C上人口数是岛A上人口数的2倍，要在海岸线（曲线PQ）上建一个码头，使由该码头运往岛A、岛C的给养运费最少，问码头应建在何处？
解：以BC所在直线为x轴，BC的垂直平分线为y轴建立坐标系如图所示. 设曲线PQ上任一点P(x,y). ∵海岸线（曲线PQ）上任一点到岛B、C的距离和是常数8海里＞4海里=|BC|， ∴曲线PQ的形状是椭圆. 则2a=8,2c=4. ∴a=4,c=2,b= ∴曲线PQ的方程是 那么2|PC|等于P到右准线l的距离|PD|，即|PD|=2|PC|. 则|PA|+2|PC|=|PA|+|PD|. ∴当P、A、D三点共线时，即PA⊥l时， |PA|+2|PC|取最小值，此时P(2 由以上所得，要使码头运往岛A、C的给养费最少，码头应建在A岛正东(2+2
=
=2
,e=
.
+
=1.
,
).
)海里处.
练习册系列答案
青苹果同步评价手册系列答案
初中英语知识集锦系列答案
小学语文词语手册吉林教育出版社系列答案
初中总复习中考精编系列答案
创新金卷毕业升学系列答案
创新课时训练系列答案
创新学案课时学练测系列答案
创新学习三级训练系列答案
创新与探究系列答案
达标测试卷系列答案
相关题目
，
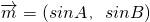=（cosB，-cosA）且
．
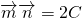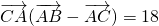，求边c的长．
，
=（cosB，-cosA）且
．
，求边c的长．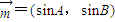
，
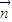=（cosB，-cosA）且
．
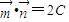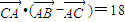，求边c的长．