题目内容
函数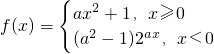 ,在(-∞,+∞)上单调递增,则a的取值范围是
,在(-∞,+∞)上单调递增,则a的取值范围是
- A.(-∞,-
 ]∪(1,
]∪(1, ]
] - B.( 1,
 ]
] - C.[-
 ,-1)∪[
,-1)∪[ ,+∞)
,+∞) - D.[
 ,+∞)
,+∞)
B
分析:先分区间使函数f(x)在每个区间上都单调递增,再保证(a2-1)2a×0≤a×02+1,解出a的范围取交集即可.
解答:因为函数f(x)在(-∞,+∞)上单调递增,
则①当x≥0时,f(x)=ax2+1是单调递增函数,所以a>0.
②当x<0时,f(x)=(a2-1)2ax是单调递增函数,所以f′(x)=aln2•(a2-1)2ax≥0,
因为a>0,所以a≥1.
当a=1时f(x)=0不具有单调性,所以a=1舍去,所以a>1.
又函数f(x)在(-∞,+∞)上单调递增,
所以(a2-1)2a×0≤a×02+1,解得- ≤a≤
≤a≤ .
.
由以上可得1<a≤ ,即a的取值范围为(1,
,即a的取值范围为(1, ].
].
故选B.
点评:本题考查函数单调性的性质,解决这种分段函数单调性问题的关键是先分区间保证函数单调,再保证最值之间满足大小关系即可.
分析:先分区间使函数f(x)在每个区间上都单调递增,再保证(a2-1)2a×0≤a×02+1,解出a的范围取交集即可.
解答:因为函数f(x)在(-∞,+∞)上单调递增,
则①当x≥0时,f(x)=ax2+1是单调递增函数,所以a>0.
②当x<0时,f(x)=(a2-1)2ax是单调递增函数,所以f′(x)=aln2•(a2-1)2ax≥0,
因为a>0,所以a≥1.
当a=1时f(x)=0不具有单调性,所以a=1舍去,所以a>1.
又函数f(x)在(-∞,+∞)上单调递增,
所以(a2-1)2a×0≤a×02+1,解得-
 ≤a≤
≤a≤ .
.由以上可得1<a≤
 ,即a的取值范围为(1,
,即a的取值范围为(1, ].
].故选B.
点评:本题考查函数单调性的性质,解决这种分段函数单调性问题的关键是先分区间保证函数单调,再保证最值之间满足大小关系即可.

练习册系列答案
相关题目