题目内容
(2013•和平区二模)若直线x+y-m=0与曲线y=2-
有公共点,则m所的取值范围是( )
| -x(x+2) |
分析:化简所给的曲线方程,可得,它表示以M(-1,2)为圆心,半径等于1的半圆.当直线线x+y-m=0过点N(0,2)时,求得m的值;当直线x+y-m=0与半圆相切时,根据圆心到直线的距离等于半径,求得m的值,数形结合可得m的范围.
解答: 解:曲线y=2-
解:曲线y=2-
即 2-y=
,即 (x+1)2+(y-2)2=1,y≤2,
表示以M(-1,2)为圆心,半径等于1的半圆(圆位于直线y=2的部分,包括直线y=2上的点),如图所示:
当直线线x+y-m=0过点N(0,2)时,有 0+2-m=0,解得 m=2.
当直线x+y-m=0与半圆相切时,根据圆心到直线的距离等于半径可得
=1,
解得 m=1-
,或m=1+
(舍去).
故所求的m的范围为 [1-
,2],
故选B.
 解:曲线y=2-
解:曲线y=2-| -x(x+2) |
| -x(x+2) |
表示以M(-1,2)为圆心,半径等于1的半圆(圆位于直线y=2的部分,包括直线y=2上的点),如图所示:
当直线线x+y-m=0过点N(0,2)时,有 0+2-m=0,解得 m=2.
当直线x+y-m=0与半圆相切时,根据圆心到直线的距离等于半径可得
| |-1+2-m| | ||
|
解得 m=1-
| 2 |
| 2 |
故所求的m的范围为 [1-
| 2 |
故选B.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
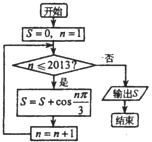 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )