Question

已知数列{a_n}的前n项和为S_n，且满足a_n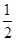＝S_n＋1（n∈N^*）；

（Ⅰ）求数列{a_n}的通项公式；

（Ⅱ）若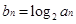，c_n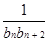＝，且{c_n}的前n项和为T_n，求使得 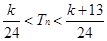对n∈N^*都成立的所有正整数k的值.

 

Answer 1

【答案】

(Ⅰ) ；(Ⅱ) .

【解析】

试题分析：(Ⅰ) 利用  ① ②

① ②得：，验证适合即得所求. 

(Ⅱ) 根据 ，利用“裂项相消法”可得

,进一步利用得到 的不等式组，

根据k是正整数，得到.

试题解析：(Ⅰ)  ①

 ②

① ②得：，又易得,             4分

(Ⅱ)   

裂项相消可得       8分

∵                       10分

∴欲对n∈N^*都成立，须，

又k正整数，∴5、6、7                          12分

考点：数列的通项公式，“裂项相消法”，不等式组的解法.