题目内容
“
”是“曲线
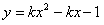恒在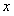
轴下方”的（ ）条件
| A．充分不必要条件 | B．必要不充分条件 | C．充要条件 | D．既非充分又非必要 |
A
解析试题分析：①k=0时，曲线y=-1恒在x轴下方；
②k≠0时，要使曲线y=kx2-kx-1恒在x轴下方，则必须满足k<0,△= k2+4k＜0，解得-4＜k＜0．
综上①②可知：曲线y=kx2-kx-1恒在x轴下方的充要条件是-4＜k
0
因此“-4＜k＜0”是“曲线y=kx2-kx-1恒在x轴下方”的充分不必要条件
故选A．
考点：充分条件的判定
点评：熟练掌握二次函数的图象与性质是解题的关键．注意分类讨论的思想方法的应用．
练习册系列答案
相关题目
下列语句中是命题的是（ ）
| A．周期函数的和是周期函数吗？ | B．梯形是不是平面图形呢？ |
C． | D． |
“
”是“
”的（ ）
| A．必要不充分条件 | B．充分不必要条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
已知
，则“
”是“
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
设
，则“
”是“
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
“
”是“
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
集合A={x||x|≤4，x∈R}，B={x|（x+5）（x-a）≤0}，则“AÍB”是“a>4”的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
是函数
在区间
上为减函数的
| A．充分非必要条件 | B．必要非充分条件 | C．充要条件 | D．非充分非必要条件 |
命题“所有实数的平方都是正数”的否定为
| A．所有实数的平方都不是正数 | B．有的实数的平方是正数 |
| C．至少有一个实数的平方是正数 | D．至少有一个实数的平方不是正数 |