题目内容
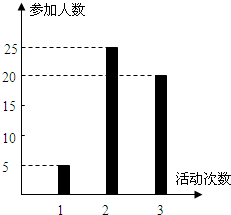按照新课程的要求，高中学生在每学期都要至少参加一次社会实践活动（以下简称活动）．某校高一•一班50名学生在上学期参加活动的次数统计如条形图所示．（ I）求该班学生参加活动的人均次数
. | x |
（ II）从该班中任意选两名学生，求他们参加活动次数恰好相等的概率；
（ III）从该班中任选两名学生，用ξ表示这两人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ．（要求：答案用最简分数表示）
分析：（ I）由图可知，参加活动1次、2次和3次的学生人数分别为5、25和20．由此能求出该班学生参加活动的人均次数．
（ II）由图可知，参加活动1次、2次和3次的学生人数分别为5、25和20．由此能求出从该班中任选两名学生，他们参加活动次数恰好相等的概率．
（ III）从该班中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件A，“这两人中一人参加2次活动，另一人参加3次活动”为事件B，“这两人中一人参加1次活动，另一人参加3次活动”为事件C．
易知P(ξ=1)=P(A)+P(B)=
+
=
；P（ξ=2）=P（C）=
=
．由此能求出ξ的分布列和ξ的数学期望．
（ II）由图可知，参加活动1次、2次和3次的学生人数分别为5、25和20．由此能求出从该班中任选两名学生，他们参加活动次数恰好相等的概率．
（ III）从该班中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件A，“这两人中一人参加2次活动，另一人参加3次活动”为事件B，“这两人中一人参加1次活动，另一人参加3次活动”为事件C．
易知P(ξ=1)=P(A)+P(B)=
| ||||
|
| ||||
|
| 25 |
| 49 |
| ||||
|
| 4 |
| 49 |
解答：解：由图可知，参加活动1次、2次和3次的学生人数分别为5、25和20．
（ I）该班学生参加活动的人均次数：
=
=
=
．
（ II）从该班中任选两名学生，
他们参加活动次数恰好相等的概率为P=
=
．
（ III）从该班中任选两名学生，
记“这两人中一人参加1次活动，另一人参加2次活动”为事件A，
“这两人中一人参加2次活动，另一人参加3次活动”为事件B，
“这两人中一人参加1次活动，另一人参加3次活动”为事件C．
易知P(ξ=1)=P(A)+P(B)=
+
=
；
P（ξ=2）=P（C）=
=
．
∴ξ的分布列：
ξ的数学期望：Eξ=0×
+1×
+2×
=
．
（ I）该班学生参加活动的人均次数：
. |
| x |
| 1×5+2×25+3×20 |
| 50 |
| 115 |
| 50 |
| 23 |
| 10 |
（ II）从该班中任选两名学生，
他们参加活动次数恰好相等的概率为P=
| ||||||
|
| 20 |
| 49 |
（ III）从该班中任选两名学生，
记“这两人中一人参加1次活动，另一人参加2次活动”为事件A，
“这两人中一人参加2次活动，另一人参加3次活动”为事件B，
“这两人中一人参加1次活动，另一人参加3次活动”为事件C．
易知P(ξ=1)=P(A)+P(B)=
| ||||
|
| ||||
|
| 25 |
| 49 |
P（ξ=2）=P（C）=
| ||||
|
| 4 |
| 49 |
∴ξ的分布列：
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 20 |
| 49 |
| 25 |
| 49 |
| 4 |
| 49 |
| 33 |
| 49 |
点评：本题考查离散型随机变量的分布列和数学期望，考查学生的运算能力，考查学生探究研究问题的能力，解题时要认真审题，理解古典概型的特征：试验结果的有限性和每一个试验结果出现的等可能性，体现了化归的重要思想．
练习册系列答案
名校课堂系列答案
相关题目
；（II）从该班中任意选两名学生，求他们参加活动次数恰好相等的概率
．
表示这两人参加活动次数之差的绝对值，求随机变量
．