题目内容
公差不为0的等差数列{an}的前n项和为Sn,若a4是a3与a7的等比中项,S8=32,则S10=________.
60
分析:设出等差数列的等差d,且d不为0,根据a4是a3与a7的等比中项,S8=32,利用等比数列的性质和等差数列的前n项和的公式化简得到关于等差数列首项和公差方程组,求出方程组的解集即可得到首项和公差,然后再利用等差数列的前n项和的公式求出S10即可.
解答:设公差为d(d≠0),则有 ,化简得:
,化简得: ,
,
因为d≠0,由①得到2a1+3d=0③,②-③得:4d=8,解得d=2,把d=2代入③求得a1=-3,
所以方程组的解集为 ,
,
则S10=10×(-3)+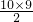 ×2=60.
×2=60.
故答案为:60
点评:此题考查学生灵活运用等差数列的前n项和的公式及等比数列的通项公式化简求值,是一道综合题.本题解法属基本量法.在解由等差(比)数列中的部分项生成等比(差)数列中部分项问题时,要特别注意新数列中项在新、老数列中的各自属性及其表示.
分析:设出等差数列的等差d,且d不为0,根据a4是a3与a7的等比中项,S8=32,利用等比数列的性质和等差数列的前n项和的公式化简得到关于等差数列首项和公差方程组,求出方程组的解集即可得到首项和公差,然后再利用等差数列的前n项和的公式求出S10即可.
解答:设公差为d(d≠0),则有
 ,化简得:
,化简得: ,
,因为d≠0,由①得到2a1+3d=0③,②-③得:4d=8,解得d=2,把d=2代入③求得a1=-3,
所以方程组的解集为
 ,
,则S10=10×(-3)+
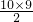 ×2=60.
×2=60.故答案为:60
点评:此题考查学生灵活运用等差数列的前n项和的公式及等比数列的通项公式化简求值,是一道综合题.本题解法属基本量法.在解由等差(比)数列中的部分项生成等比(差)数列中部分项问题时,要特别注意新数列中项在新、老数列中的各自属性及其表示.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知公差不为0的等差数列{an}满足a1,a3,a4成等比关系,Sn为{an}的前n项和,则
的值为( )
| S3-S2 |
| S5-S3 |
| A、2 | ||
| B、3 | ||
C、
| ||
| D、不存在 |