题目内容
已知函数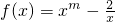 ,且
,且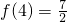 .
.
(1)求m的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
解:(1)因为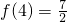 ,所以
,所以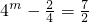 ,所以m=1.
,所以m=1.
(2)因为f(x)的定义域为{x|x≠0},又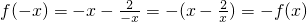 ,
,
所以f(x)是奇函数.
(3)任取x1>x2>0,则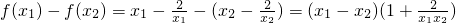 ,
,
因为x1>x2>0,所以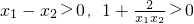 ,所以f(x1)>f(x2),
,所以f(x1)>f(x2),
所以f(x)在(0,+∞)上为单调增函数.
分析:(1)欲求m的值,只须根据f(4)= 的值,当x=4时代入f(x)解一个指数方程即可;
的值,当x=4时代入f(x)解一个指数方程即可;
(2)求出函数的定义域x|x≠0},利用奇偶性的定义判断f(x)与f(-x)的关系,即可得到答案;
(3)利用单调性的定义证明即可.任取0<x1<x2,只要证明f(x1)>f(x2),即可.
点评:本题主要考查了函数单调性的判断、函数奇偶性的判断,与证明及指数方程的解法.在判定函数奇偶性时,一定注意函数的定义域关于原点对称,属于基础题.
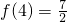 ,所以
,所以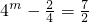 ,所以m=1.
,所以m=1.(2)因为f(x)的定义域为{x|x≠0},又
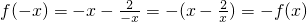 ,
,所以f(x)是奇函数.
(3)任取x1>x2>0,则
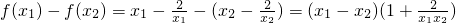 ,
,因为x1>x2>0,所以
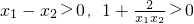 ,所以f(x1)>f(x2),
,所以f(x1)>f(x2),所以f(x)在(0,+∞)上为单调增函数.
分析:(1)欲求m的值,只须根据f(4)=
 的值,当x=4时代入f(x)解一个指数方程即可;
的值,当x=4时代入f(x)解一个指数方程即可;(2)求出函数的定义域x|x≠0},利用奇偶性的定义判断f(x)与f(-x)的关系,即可得到答案;
(3)利用单调性的定义证明即可.任取0<x1<x2,只要证明f(x1)>f(x2),即可.
点评:本题主要考查了函数单调性的判断、函数奇偶性的判断,与证明及指数方程的解法.在判定函数奇偶性时,一定注意函数的定义域关于原点对称,属于基础题.

练习册系列答案
相关题目
 ,且f(1)=2,
,且f(1)=2,
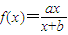 ,且f(1)=1,f(-2)=4.
,且f(1)=1,f(-2)=4. 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. (
( 且
且 )
) 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值; 的图象,写函数
的图象,写函数 (
(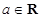 且
且 ).
). 的单调区间;
的单调区间; 的图象为曲线
的图象为曲线 .设点
.设点 ,
, 是曲线
是曲线 ,使得:①
,使得:① ;②曲线
;②曲线 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数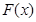 存在“中值相依切线”. 试问:函数
存在“中值相依切线”. 试问:函数 ,且
,且 ,
,
 的最大值及取得最大值时
的最大值及取得最大值时 的值。
的值。