题目内容
【题目】已知函数f(x)=|x+ ![]() |+|x﹣a|(a>0) (Ⅰ)证明:f(x)≥2
|+|x﹣a|(a>0) (Ⅰ)证明:f(x)≥2 ![]() ;
;
(Ⅱ)当a=1时,求不等式f(x)≥5的解集.
【答案】解:(Ⅰ)∵a>0, ∴f(x)=|x+ ![]() |+|x﹣a|≥|x+2a+
|+|x﹣a|≥|x+2a+ ![]() ﹣x+a|=3a+
﹣x+a|=3a+ ![]() ≥2
≥2 ![]() =2
=2 ![]() ,
,
当且仅当3a= ![]() 即a=
即a= ![]() 时”=“成立;
时”=“成立;
(Ⅱ)a=1时,f(x)=|x+3|+|x﹣1|≥5,
x≥1时,x+3+x﹣1≥5,解得:x≥ ![]() ,
,
﹣3<x<1时,x+3+1﹣x=4≥5,无解,
x≤﹣3时,﹣x﹣3﹣x+1=﹣2x﹣2≥5,解得:x≤﹣ ![]() ,
,
故不等式的解集是{x|x≥ ![]() 或x≤﹣
或x≤﹣ ![]() }
}
【解析】(Ⅰ)根据绝对值的性质以及基本不等式的性质证明即可;(Ⅱ)将a的值代入,通过讨论x的范围求出不等式的解集即可.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

 智能训练练测考系列答案
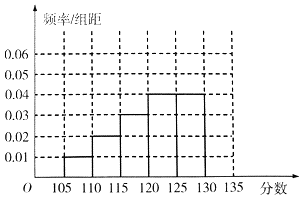
智能训练练测考系列答案【题目】某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
第一组 | [105,110] | 15 | 0.3 |
第二组 | [110,115) | 30 | 0.3 |
第三组 | [115,120) | x | 0.4 |
第四组 | [120,125) | 100 | 0.5 |
第五组 | [125,130) | 120 | 0.6 |
第六组 | [130,135) | 195 | y |
(Ⅰ)补全所给的频率分布直方图,并求n,x,y的值;
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.