题目内容
设 、
、 、
、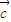 是任意的非零平面向量,且相互不共线,则( )
是任意的非零平面向量,且相互不共线,则( )①
 -
-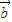 =0;
=0;②|
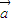 |-|
|-|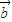 |<|
|<|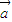 -
-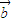 |;
|;③
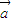 -
-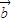 不与
不与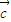 垂直;
垂直;④(3
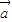 +2
+2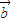 )•(3
)•(3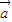 -2
-2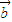 )=9|
)=9|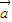 |2-4|
|2-4|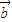 |2.
|2.其中的真命题是( )
A.②④
B.③④
C.②③
D.①②
【答案】分析:利用向量的基本知识进行分析转化是解决本题的关键.根据向量的数乘运算、向量的数量积运算性质,向量减法的几何意义对有关问题进行求解并加以判断.
解答:解:由于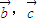 是不共线的向量,因此(
是不共线的向量,因此(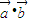 )
)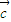 不一定等于(
不一定等于(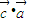 )
)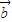 ,故①错误;
,故①错误;
由于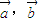 不共线,故
不共线,故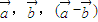 构成三角形,因此②正确;
构成三角形,因此②正确;
由于[(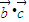 )
)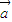 -(
-(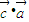 )
)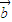 ]
] =
=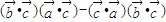 =0,故③中两向量垂直,故③错误;
=0,故③中两向量垂直,故③错误;
根据向量数量积的运算可以得出④是正确的.故选A.
点评:本题考查平面向量的基本运算性质,数量积的运算性质,考查向量问题的基本解法,等价转化思想.要区分向量运算与数的运算.避免类比数的运算进行错误选择.
解答:解:由于
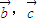 是不共线的向量,因此(
是不共线的向量,因此(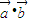 )
)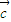 不一定等于(
不一定等于(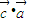 )
)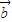 ,故①错误;
,故①错误;由于
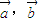 不共线,故
不共线,故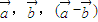 构成三角形,因此②正确;
构成三角形,因此②正确;由于[(
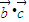 )
)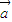 -(
-(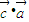 )
)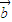 ]
] =
=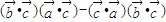 =0,故③中两向量垂直,故③错误;
=0,故③中两向量垂直,故③错误;根据向量数量积的运算可以得出④是正确的.故选A.
点评:本题考查平面向量的基本运算性质,数量积的运算性质,考查向量问题的基本解法,等价转化思想.要区分向量运算与数的运算.避免类比数的运算进行错误选择.

练习册系列答案
相关题目