题目内容
设函数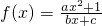
是奇函数（a，b，c都是整数），且f（1）=2，f（2）＜3．求a，b，c的值．
解：由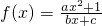是奇函数，
得f（-x）=-f（x）对定义域内x恒成立，
则
对定义域内x恒成立，
即c=0． …4
（或由定义域关于原点对称得c=0）
又
…8
由①得a=2b-1代入②得
，…10
又a，b，c是整数，得b=a=1．…12
分析：根据函数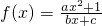是奇函数，f（-x）=-f（x）对定义域内x恒成立，可求出c值，代入f（1）=2，f（2）＜3，可求出a，b的值．
点评：本题考查的知识点是函数的奇偶性，不等式的解法，其中根据已知构造对应的方程或不等式是解答的关键．
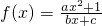是奇函数，得f（-x）=-f（x）对定义域内x恒成立，
则
对定义域内x恒成立，
即c=0． …4
（或由定义域关于原点对称得c=0）
又
…8由①得a=2b-1代入②得
，…10又a，b，c是整数，得b=a=1．…12
分析：根据函数
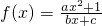是奇函数，f（-x）=-f（x）对定义域内x恒成立，可求出c值，代入f（1）=2，f（2）＜3，可求出a，b的值．点评：本题考查的知识点是函数的奇偶性，不等式的解法，其中根据已知构造对应的方程或不等式是解答的关键．
练习册系列答案
相关题目
是奇函数（a，b，c都是整数），且
，
的单调性如何？用单调性定义证明你的结论。
是奇函数（a，b，c都是整数），且
，
的单调性如何？用单调性定义证明你的结论。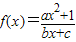
是奇函数（a，b，c都是整数），且f（1）=2，f（2）＜3．求a，b，c的值．
的定义域为D，若存在非零实数
使得对于任意
，有
，且
，则称
时，
，且
的取值范围是
B． 
C．
D．