题目内容
数列{an}的前n项和为sn,Sn+an=- n2-
n2- n+1(n∈N﹡).
n+1(n∈N﹡).(Ⅰ)设bn=an+n,证明:数列{bn}是等比数列;
(Ⅱ)求数列{nbn}的前n项和Tn.
【答案】分析:(Ⅰ)由Sn+an=- n2-
n2- n+1知,n=1时可求得a1;当n≥2时,有an-1+Sn-1=-
n+1知,n=1时可求得a1;当n≥2时,有an-1+Sn-1=- (n-1)2-
(n-1)2- (n-1)+1,两式相减可求得bn=
(n-1)+1,两式相减可求得bn= bn-1(n≥2),利用等比数列的定义可证数列{bn}是等比数列;
bn-1(n≥2),利用等比数列的定义可证数列{bn}是等比数列;
(Ⅱ)由(Ⅰ)知bn=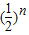 ,Tn=
,Tn= +
+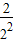 +
+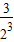 +
+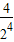 +…+
+…+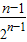 +
+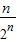 ,利用错位相减法即可求得Tn.
,利用错位相减法即可求得Tn.
解答:解:(Ⅰ)因为Sn+an=- n2-
n2- n+1,
n+1,
所以①当n=1时,2a1=-1,则a1=- ,…(1分)
,…(1分)
②当n≥2时,an-1+Sn-1=- (n-1)2-
(n-1)2- (n-1)+1,…(2分)
(n-1)+1,…(2分)
所以2an-an-1=-n-1,即2(an+n)=an-1+n-1,…(4分)
所以bn= bn-1(n≥2),而b1=a1+1=
bn-1(n≥2),而b1=a1+1= ,…(5分)
,…(5分)
所以数列{bn}是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以bn=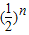 .…(6分)
.…(6分)
(Ⅱ)由(Ⅰ)得nbn=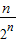 .
.
所以Tn= +
+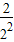 +
+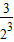 +
+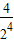 +…+
+…+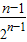 +
+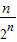 ①,
①,
2Tn=1+ +
+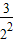 +
+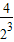 +…+
+…+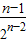 +
+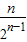 ②,…(8分)
②,…(8分)
②-①得:Tn=1+ +
+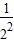 +…+
+…+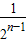 -
-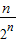 …(10分)
…(10分)
=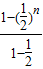 -
-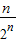
=2-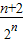 .…(12分)
.…(12分)
点评:本题考查数列的求和,考查等比关系的确定,突出考查错位相减法求和的应用,考查转化思想与运算能力,属于中档题.
 n2-
n2- n+1知,n=1时可求得a1;当n≥2时,有an-1+Sn-1=-
n+1知,n=1时可求得a1;当n≥2时,有an-1+Sn-1=- (n-1)2-
(n-1)2- (n-1)+1,两式相减可求得bn=
(n-1)+1,两式相减可求得bn= bn-1(n≥2),利用等比数列的定义可证数列{bn}是等比数列;
bn-1(n≥2),利用等比数列的定义可证数列{bn}是等比数列;(Ⅱ)由(Ⅰ)知bn=
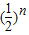 ,Tn=
,Tn= +
+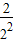 +
+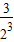 +
+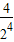 +…+
+…+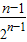 +
+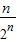 ,利用错位相减法即可求得Tn.
,利用错位相减法即可求得Tn.解答:解:(Ⅰ)因为Sn+an=-
 n2-
n2- n+1,
n+1,所以①当n=1时,2a1=-1,则a1=-
 ,…(1分)
,…(1分)②当n≥2时,an-1+Sn-1=-
 (n-1)2-
(n-1)2- (n-1)+1,…(2分)
(n-1)+1,…(2分)所以2an-an-1=-n-1,即2(an+n)=an-1+n-1,…(4分)
所以bn=
 bn-1(n≥2),而b1=a1+1=
bn-1(n≥2),而b1=a1+1= ,…(5分)
,…(5分)所以数列{bn}是首项为
 ,公比为
,公比为 的等比数列,
的等比数列,所以bn=
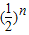 .…(6分)
.…(6分)(Ⅱ)由(Ⅰ)得nbn=
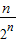 .
.所以Tn=
 +
+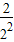 +
+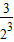 +
+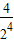 +…+
+…+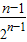 +
+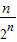 ①,
①,2Tn=1+
 +
+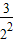 +
+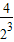 +…+
+…+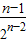 +
+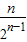 ②,…(8分)
②,…(8分)②-①得:Tn=1+
 +
+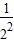 +…+
+…+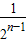 -
-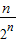 …(10分)
…(10分)=
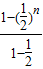 -
-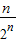
=2-
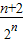 .…(12分)
.…(12分)点评:本题考查数列的求和,考查等比关系的确定,突出考查错位相减法求和的应用,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目