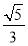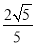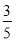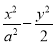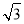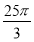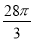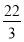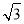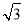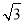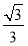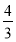Question

已知数列{an}的前n项和是Sn，且Sn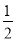＋an＝1.

(1)求数列{an}的通项公式；

(2)记bn＝log3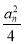，数列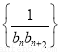的前n项和为Tn，证明：Tn<.

 

Answer 1

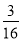（1）2×3－n（2）见解析

【解析】(1)当n＝1时，a1＝S1，由S1＋a1＝1，

解得a1＝当n≥2时，∵Sn＝1－an，Sn－1＝1－an－1，∴Sn－Sn－1＝ (an－1－an)，即an＝ (an－1－an)．

∴an＝an－1.∴{an}是以为首项，为公比的等比数列，其通项公式为an＝×n－1＝2×3－n.

(2)∵bn＝log3＝2 log33－n＝－2n.

∴

 

∴Tn＝＝＝<.