题目内容
已知常数a>0,向量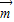 =(0,a),
=(0,a),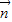 =(1,0)经过定点A(0,-a)以
=(1,0)经过定点A(0,-a)以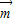 +
+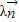 为方向向量的直线与经过定点B(0,a)以
为方向向量的直线与经过定点B(0,a)以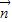 +2
+2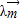 为方向向量的直线相交于点P,其中λ∈R.
为方向向量的直线相交于点P,其中λ∈R.(I)求点P的轨迹C的方程;
(Ⅱ)若a=
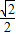 ,过E(0,1)的直线l交曲线C于M、N两点,求
,过E(0,1)的直线l交曲线C于M、N两点,求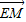 •
•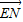 的取值范围.
的取值范围.
【答案】分析:(I)利用向量共线定理和坐标运算即可得出;
(II)对直线l的斜率分类讨论,当直线l的斜率存在时,设直线l的方程为y=kx+1与双曲线的方程联立,即可得到根与系数的关系,再利用向量的数量积和对k分类讨论即可得出.
解答:解:(I)设P(x,y),∴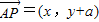 ,
,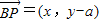 .
.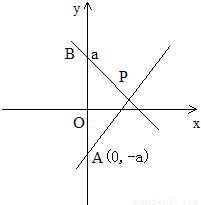
又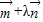 =(0,a)+λ(1,0)=(λ,a),
=(0,a)+λ(1,0)=(λ,a),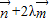 =(1,0)+2λ(0,a)=(1,2λa),
=(1,0)+2λ(0,a)=(1,2λa),
∵(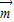 +
+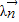 )
)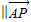 ,(
,(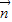 +2
+2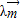 )
)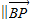 ,
,
∴xa-λ(y+a)=0,2λax-(y-a)=0,
消去参数λ得y2-2a2x2=a2.
化为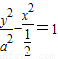 .
.
(II)当a=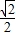 时,点P的轨迹方程为
时,点P的轨迹方程为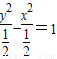 .
.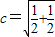 =1.
=1.
∴E(0,1)为双曲线的一焦点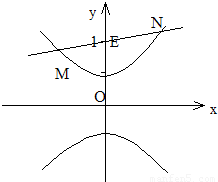 .
.
①当直线l的斜率不存在时,其方程为x=0,l与双曲线分别相较于点M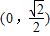 ,N
,N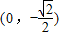 .此时
.此时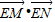 =
=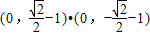 =
= .
.
②当直线l的斜率存在时,设l的方程为y=kx+1,代入双曲线得2(k2-1)x2+4kx+1=0,
∵l与双曲线交于两点,∴△=16k2-8(k2-1)>0,且k2-1≠0.
设两交点为M(x1,y1),N(x2,y2).
则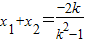 ,
,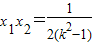 .
.
∴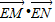 =(x1,y1-1)•(x2,y2-1)=
=(x1,y1-1)•(x2,y2-1)=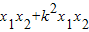 =
=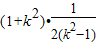 =
=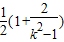 .
.
当-1<k<1时,k2-1<0,则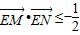 ,
,
当k<-1或k>1时,k2-1>0,故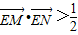 .
.
综上所述: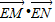 的取值范围是
的取值范围是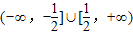 .
.
点评:熟练掌握向量共线定理和坐标运算、分类讨论、直线与双曲线相交问题转化为方程联立得到根与系数的关系、向量的数量积运算等是解题的关键.
(II)对直线l的斜率分类讨论,当直线l的斜率存在时,设直线l的方程为y=kx+1与双曲线的方程联立,即可得到根与系数的关系,再利用向量的数量积和对k分类讨论即可得出.
解答:解:(I)设P(x,y),∴
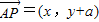 ,
,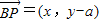 .
.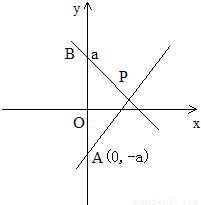
又
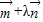 =(0,a)+λ(1,0)=(λ,a),
=(0,a)+λ(1,0)=(λ,a),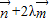 =(1,0)+2λ(0,a)=(1,2λa),
=(1,0)+2λ(0,a)=(1,2λa),∵(
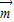 +
+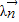 )
)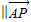 ,(
,(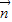 +2
+2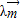 )
)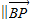 ,
,∴xa-λ(y+a)=0,2λax-(y-a)=0,
消去参数λ得y2-2a2x2=a2.
化为
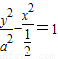 .
.(II)当a=
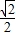 时,点P的轨迹方程为
时,点P的轨迹方程为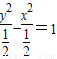 .
.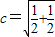 =1.
=1.∴E(0,1)为双曲线的一焦点
 .
.①当直线l的斜率不存在时,其方程为x=0,l与双曲线分别相较于点M
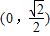 ,N
,N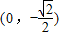 .此时
.此时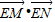 =
=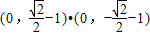 =
= .
.②当直线l的斜率存在时,设l的方程为y=kx+1,代入双曲线得2(k2-1)x2+4kx+1=0,
∵l与双曲线交于两点,∴△=16k2-8(k2-1)>0,且k2-1≠0.
设两交点为M(x1,y1),N(x2,y2).
则
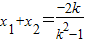 ,
,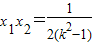 .
.∴
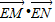 =(x1,y1-1)•(x2,y2-1)=
=(x1,y1-1)•(x2,y2-1)=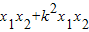 =
=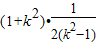 =
=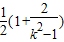 .
.当-1<k<1时,k2-1<0,则
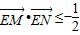 ,
,当k<-1或k>1时,k2-1>0,故
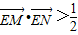 .
.综上所述:
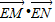 的取值范围是
的取值范围是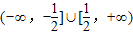 .
.点评:熟练掌握向量共线定理和坐标运算、分类讨论、直线与双曲线相交问题转化为方程联立得到根与系数的关系、向量的数量积运算等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =(0,a),
=(0,a), =(1,0),经过原点O以
=(1,0),经过原点O以 +λ
+λ ,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由. =(0,a),
=(0,a), =(1,0),经过原点O以
=(1,0),经过原点O以 +λ
+λ ,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
,为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.