题目内容
设向量a,b满足|a|=|b|=1及|3a-2b|= .
.
(1)求a,b夹角的大小;
(2)求|3a+b|的值.
 .
.(1)求a,b夹角的大小;
(2)求|3a+b|的值.
(1)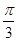 (2)
(2)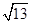
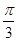 (2)
(2)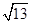
解:(1)设a与b夹角为θ,(3a-2b)2=7,
即9|a|2+4|b|2-12a·b=7,
而|a|=|b|=1,
∴a·b=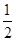 ,
,
∴|a||b|cosθ=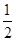 ,即cosθ=
,即cosθ=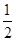 ,
,
又θ∈[0,π],∴a,b的夹角为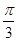 .
.
(2)(3a+b)2=9|a|2+6a·b+|b|2=9+3+1=13,
∴|3a+b|=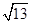 .
.
即9|a|2+4|b|2-12a·b=7,
而|a|=|b|=1,
∴a·b=
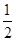 ,
,∴|a||b|cosθ=
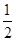 ,即cosθ=
,即cosθ=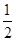 ,
,又θ∈[0,π],∴a,b的夹角为
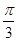 .
.(2)(3a+b)2=9|a|2+6a·b+|b|2=9+3+1=13,
∴|3a+b|=
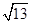 .
.
练习册系列答案
相关题目
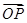 ·
·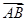 的最小值为________.
的最小值为________.
 ,求
,求 的值;
的值; ,其中
,其中 为坐标原点,求
为坐标原点,求 的值.
的值.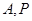 为椭圆
为椭圆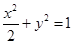 上两点.点
上两点.点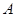 关于
关于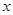 轴对称点为
轴对称点为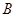 (异于点
(异于点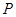 ).若直线
).若直线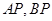 分别与
分别与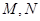 , 则
, 则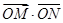 =( )
=( )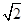
 )·(
)·( )=0,则点P的轨迹一定过△ABC的( )
)=0,则点P的轨迹一定过△ABC的( ) 与
与 垂直,且
垂直,且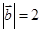 ,则
,则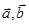 满足
满足 ,
, ,则
,则 ( )
( ) 满足:
满足: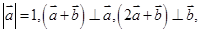 则
则


 、
、 ,满足
,满足 ,
, ,则
,则 .
.