题目内容
（本小题满分12分）已知函数
（1） 求函数
的单调区间和极值；
（2） 求证：当
时，
（3） 如果
，且
，求证：
设
则
可知
在区间
单调递增，
在区间
单调递减。
所以，当
有最大值
所以，当
的面积有最大值
…………14分
解法二：（II）设直线AB的方程为
由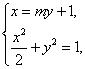
可得
，
记
中点
则
可得
…………6分
垂直平分线NG的方程为
令y=0，得
…………8分
的取值范围为
…………10分
（III）
而
由
所以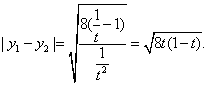
又|F2G|=1-t，
所以
所以
的面积为
…………11分
下同解法一：
设
则
可知在区间单调递增，
在区间单调递减。
所以，当
有最大值
所以，当的面积有最大值 …………12分
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
