题目内容
已知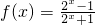 .
.
(1)讨论f(x)的奇偶性;
(2)讨论f(x)的单调性.
解:(1)f(x)的定义域为R
∵f(-x)= =
= =-
=- =-f(x)
=-f(x)
∴f(x)是奇函数…(6分)
(2)任取x1、x2∈R,且x1<x2,则
f(x1)-f(x2)=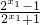 -
- =
=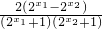
∵x1<x2,可得 <
< ,且
,且 +1>0,
+1>0, +1>0
+1>0
∴f(x1)-f(x2)<0,可得f(x1)<f(x2)
所以函数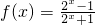 是(-∞,+∞)上的增函数.
是(-∞,+∞)上的增函数.
分析:(1)根据奇偶性的定义,将函数f(-x)化简整理,可得f(-x)=-f(x),所以f(x)在其定义域上是奇函数;
(2)利用函数单调性的定义,取x1、x2∈R,且x1<x2,通过作差因式分解,得到f(x1)<f(x2),所以f(x)是R上的增函数.
点评:本题给出含有指数式的分式函数,讨论函数的奇偶性和单调性,着重考查了函数的单调性和奇偶性的定义、基本初等函数性质等知识,属于中档题.
∵f(-x)=
 =
= =-
=- =-f(x)
=-f(x)∴f(x)是奇函数…(6分)
(2)任取x1、x2∈R,且x1<x2,则
f(x1)-f(x2)=
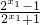 -
- =
=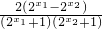
∵x1<x2,可得
 <
< ,且
,且 +1>0,
+1>0, +1>0
+1>0∴f(x1)-f(x2)<0,可得f(x1)<f(x2)
所以函数
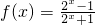 是(-∞,+∞)上的增函数.
是(-∞,+∞)上的增函数.分析:(1)根据奇偶性的定义,将函数f(-x)化简整理,可得f(-x)=-f(x),所以f(x)在其定义域上是奇函数;
(2)利用函数单调性的定义,取x1、x2∈R,且x1<x2,通过作差因式分解,得到f(x1)<f(x2),所以f(x)是R上的增函数.
点评:本题给出含有指数式的分式函数,讨论函数的奇偶性和单调性,着重考查了函数的单调性和奇偶性的定义、基本初等函数性质等知识,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
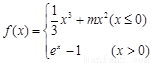
 .
.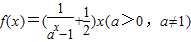 .
. .
.