题目内容
(2012•孝感模拟)数列{an}的前n项和Sn=npan(n∈N*),并且a1≠a2.
(I)求P的值;
(II)作函数f(x)=a2x2+a3x2+…+an+1xn,如果S10=45,证明:,f(
)<
.
(I)求P的值;
(II)作函数f(x)=a2x2+a3x2+…+an+1xn,如果S10=45,证明:,f(
| 1 |
| 3 |
| 3 |
| 4 |
分析:(I)由Sn=npan(n∈N*),得到a1=0,a2≠0,由此能求出p.
(II)由Sn+1=
(n+1)an+1,Sn=
nan,知an+1=
(n+1)an+1-
nan,由此导出f(
)=
+
+…+
,再由错位相减法能够证明f(
)<
.
(II)由Sn+1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 32 |
| n |
| 3n |
| 1 |
| 3 |
| 3 |
| 4 |
解答:解:(I)∵Sn=npan(n∈N*),
∴a1=S1=pa1,若a1≠0,则p=1,
由a1+a2=S2=2pa2,
得a1=a2,矛盾,故a1=0,a2≠0,
∵a1+a2=S2=2pa2,
∴p=
.
(II)∵Sn+1=
(n+1)an+1,Sn=
nan,
∴an+1=
(n+1)an+1-
nan,
(n-1)an+1=nan,
当k≥2时,
=
,
∴n≥3时,有an=
×
×…×
×a2=(n-1)a2,
∴对一切n∈N*,有an=(n-1)a2,
∵45=S10=10×
×a10=45a2,
∴a2=1,an=n-1(n∈N*),
故f(x)=x+2x2+…+nxn,
∴f(
)=
+
+…+
,
f(
)=
+
+…+
,
∴
f(
)=
+
+…+
-
,
∴f(
)=
-
,
故f(
)<
.
∴a1=S1=pa1,若a1≠0,则p=1,
由a1+a2=S2=2pa2,
得a1=a2,矛盾,故a1=0,a2≠0,
∵a1+a2=S2=2pa2,
∴p=
| 1 |
| 2 |
(II)∵Sn+1=
| 1 |
| 2 |
| 1 |
| 2 |
∴an+1=
| 1 |
| 2 |
| 1 |
| 2 |
(n-1)an+1=nan,
当k≥2时,
| ak+1 |
| ak |
| k |
| k-1 |
∴n≥3时,有an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a3 |
| a2 |
∴对一切n∈N*,有an=(n-1)a2,
∵45=S10=10×
| 1 |
| 2 |
∴a2=1,an=n-1(n∈N*),
故f(x)=x+2x2+…+nxn,
∴f(
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 32 |
| n |
| 3n |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 2 |
| 33 |
| n |
| 3n+1 |
∴
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| n |
| 3n+1 |
∴f(
| 1 |
| 3 |
| 3 |
| 4 |
| 2n+3 |
| 4×3n |
故f(
| 1 |
| 3 |
| 3 |
| 4 |
点评:本题考查数列的综合运用,有一定的探索性,对数学思想的要求较高,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意错位相减法的合理运用.

练习册系列答案
相关题目
 (2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
(2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )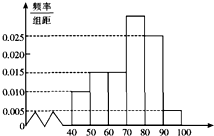 (2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题: