题目内容
设锐角 的三内角
的三内角 、
、 、
、 所对边的边长分别为
所对边的边长分别为 、
、 、
、 ,且
,且 ,
, ,则
,则 的取值范围为( ).
的取值范围为( ).
A. | B. | C. . . | D.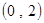 |
A
解析试题分析:要求 的范围,首先用正弦定理建立一个关系,
的范围,首先用正弦定理建立一个关系,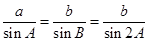 ,从而
,从而 ,因此我们只要确定出
,因此我们只要确定出 的取值范围,就可求出
的取值范围,就可求出 的取值范围了,
的取值范围了,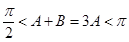 ,从而
,从而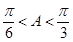 ,又
,又 ,
,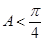 ,所以有
,所以有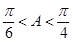 ,
,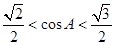 ,所以
,所以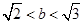 .
.
考点:正弦定理,锐角三角形的判定.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知 中
中 的对边分别为
的对边分别为 若
若 且
且 ,则
,则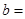 ( )
( )
| A.2 | B.4+ | C.4— | D. |
在 ABC中,若
ABC中,若 、
、 的对边长分别为b、c,
的对边长分别为b、c, ,
,
 ,则
,则 ( )
( )
A. | B. | C. | D. 或 或 |
边长为 的三角形的最大角与最小角的和是( )
的三角形的最大角与最小角的和是( )
A. | B. | C. | D. |
在等腰△ 中,
中, 是腰
是腰 的中点,若
的中点,若 ,则
,则 ( )
( )
A. | B. | C. | D. |
在 中,若
中,若 ,则
,则 的形状是( )
的形状是( )
| A.正三角形 | B.等腰三角形 |
| C.直角三角形 | D.等腰直角形 |
若△ABC的三边为a,b,c,它的面积为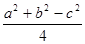 ,则内角C等于( )
,则内角C等于( )
| A.30° | B.45° | C.60° | D.90° |
在 中,
中, ,那么
,那么 是( )
是( )
| A.直角三角形 | B.等腰三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
 中,角A.B.C所对的边分别是
中,角A.B.C所对的边分别是 .
. .
. ,若
,若 ,
, ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.