Question

已知抛物线的顶点在原点，焦点在坐标轴上，又知此抛物线上的一点A（m,-3）到焦点F的距离为5，求抛物线的方程及m的值.

Answer 1

分析：应先确定抛物线方程的形式，再确定p值.

解：（1）若抛物线的开口向下，设抛物线方程为x²=-2py(p＞0).此时，准线方程为y=,从定义知-(-3)=5,解得p=4.

所以抛物线方程为x²=-8y,此时m=±2.

(2)若抛物线开口向左或向右，可设抛物线方程为y²=2ax(a≠0)

准线方程为x=-,由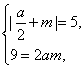

解得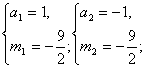

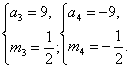
所以有y²=2x,m=;或y²=-2x,m=-;y²=18x,m=;y²=-18x,m=-.

点拨：在不能确定抛物线开口方向时，抛物线的标准方程可设为y²=2ax(a≠0)或x²=2ay(a≠0).解出a值，由a值来确定焦点位置.