题目内容
设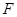 为双曲线
为双曲线 的左焦点,在
的左焦点,在 轴上
轴上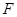 点的右侧有一点
点的右侧有一点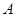 ,以
,以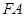 为直径的圆与双曲线左、右两支在
为直径的圆与双曲线左、右两支在 轴上方的交点分别为
轴上方的交点分别为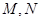 ,则
,则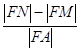 的值为( )
的值为( )
A. | B.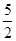 | C.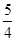 | D.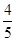 |
D.
解析试题分析:设 (m>4),F(-5,0).所以
(m>4),F(-5,0).所以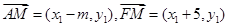 .因为
.因为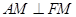 ,所以
,所以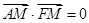 .即
.即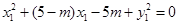 ,又因为点M在双曲线上,所以
,又因为点M在双曲线上,所以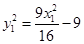 .代入前式可得
.代入前式可得 .即
.即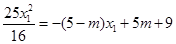 .同理由N点的关系式可得
.同理由N点的关系式可得 .所以由椭圆和圆联立可得方程
.所以由椭圆和圆联立可得方程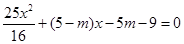 ,所以.
,所以.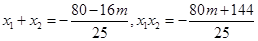 .又因为
.又因为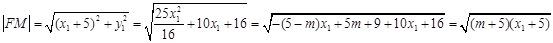 .同理
.同理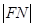 =
= .又因为
.又因为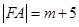 .所以
.所以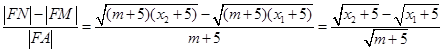 .所以
.所以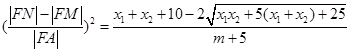 =
= .所以
.所以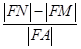 =
=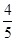 .故选D.本题的解法较麻烦,运算量较大.主要是通过FM与AM垂直,得到的式子与FN与AN垂直得到的式子抽象出椭圆与圆的交点方程.再用韦达定理表示出FM与FN的长.再把所求的式子平方即可得到答案.
.故选D.本题的解法较麻烦,运算量较大.主要是通过FM与AM垂直,得到的式子与FN与AN垂直得到的式子抽象出椭圆与圆的交点方程.再用韦达定理表示出FM与FN的长.再把所求的式子平方即可得到答案.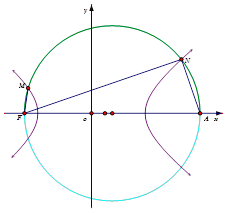
考点:1.向量的垂直.2.两点间的距离的表示.3.韦达定理的应用.4.较繁杂的代数运算.

练习册系列答案
相关题目
已知动点 的坐标满足方程
的坐标满足方程 ,则
,则 的轨迹方程是( )
的轨迹方程是( )
A. | B. |
C. | D.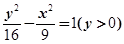 |
抛物线 上两点
上两点 、
、 关于直线
关于直线 对称,且
对称,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知双曲线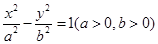 的离心率
的离心率 ,则它的渐近线方程为( )
,则它的渐近线方程为( )
A.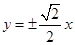 | B.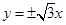 | C.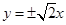 | D.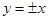 |
已知抛物线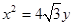 的准线过双曲线
的准线过双曲线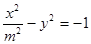 的一个焦点,则双曲线的离心率为( )
的一个焦点,则双曲线的离心率为( )
A.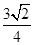 | B.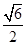 | C. | D.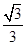 |
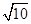 ,0)、F2(
,0)、F2(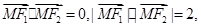 则该双曲线的方程是( )
则该双曲线的方程是( )
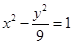
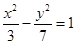
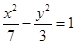
 中,
中,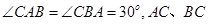 边上的高分别为
边上的高分别为 ,垂足分别是
,垂足分别是 ,则以
,则以 为焦点且过
为焦点且过 ,则
,则 的值为( )
的值为( )




 的焦点
的焦点 与椭圆
与椭圆 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为 ,且
,且 与
与 轴垂直,则椭圆的离心率为( )
轴垂直,则椭圆的离心率为( ) 

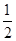


 与双曲线
与双曲线 有相同的焦点F,点
有相同的焦点F,点 是两曲线的交点,且
是两曲线的交点,且 轴,则
轴,则 的值为( )
的值为( )


