Question

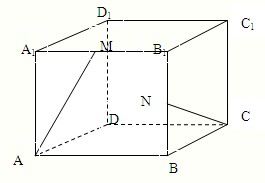（2007•上海模拟）在正方体ABCD-A₁B₁C₁D₁中，棱长为a，M为A₁B₁的中点，N为BB₁的中点．
（1）求异面直线AM与CN所成角的大小；
（2）求四面体N-AMC的体积．

Answer 1

分析：（1）利用空间向量求异面直线所成角，就是把异面直线所成角转化为空间向量的夹角，本题中，建立空间直角坐标系，异面直线AM与CN所成角即

AM

与

CN

的夹角，再用向量的夹角公式计算即可．
（2）欲求四面体N-AMC的体积，只需用割补法，把四面体N-AMC看做以△AMN为底面，以CB为高，利用三棱锥的体积公式计算即可．

解答：解：（1）以D为坐标原点，以DA，DC，DD₁分别为x轴y轴z轴建立空间直角坐标系
则 A（a，0，0）C（0，a，0）M(a，

a

2

，a)N(a，a，

a

2

)
∴

AM

={0，

a

2

，a}，

CN

={a，0，

a

2

}
设

AM

与

CN

夹角为θ，COSθ=

AM CN

| AM || CN |

=

1 2 a2

5 4 a2

=

2

5

∴θ=arccos

2

5

∴异面直线AM与CN所成角为arccos

2

5

  
（2）VN-AMC=VC-AMN=

1

3

S△AMNCB
而S△AMN=SABB1A1-S△AMA1-S△ABN-S△B1MN=a2-

1

4

a2-

1

4

a2-

1

8

a2=

3

8

a2
∴V=

1

3

×

3

8

a2×a=

1

8

a3

点评：本题主要考查了利用空间向量求异面直线所成角，以及三棱锥体积公式的应用．