题目内容
（文科）已知直线
，过点P的直线m与直线l在第一象限交于点Q，与x轴交于点M，若△OMQ为等边三角形．
（I）求点Q的坐标；
（II）求△OMQ的内切圆方程．
解：（I）因为直线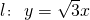
的倾斜角为60°，要使△OMQ为等边三角形，直线m的斜率应为
设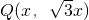
，则
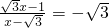，解得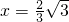
，∴
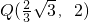
（II）由（I）得直线m的方程为
令y=0，得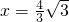
∴
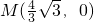
∵等边三角形的内切圆的圆心，也是三角形的重心
设圆心坐标为（x，y）
∴根据三角形的重心坐标公式可得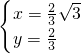
又半径为
∴所求圆的方程为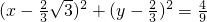
分析：（I）因为直线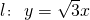的倾斜角为60°，要使△OMQ为等边三角形，直线m的斜率应为，利用斜率公式可求点Q的坐标；
（II）由于等边三角形的内切圆的圆心，也是三角形的重心，故可利用重心坐标公式，求出圆心坐标，从而得到圆的方程．
点评：本题以直线为载体，考查直线的斜率公式，考查圆的方程，属于中档题．
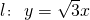的倾斜角为60°，要使△OMQ为等边三角形，直线m的斜率应为设
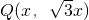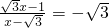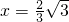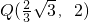
，则，解得，∴（II）由（I）得直线m的方程为
令y=0，得
∴
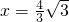
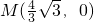
∵等边三角形的内切圆的圆心，也是三角形的重心
设圆心坐标为（x，y）
∴根据三角形的重心坐标公式可得
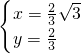
又半径为
∴所求圆的方程为
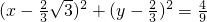
分析：（I）因为直线
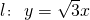的倾斜角为60°，要使△OMQ为等边三角形，直线m的斜率应为，利用斜率公式可求点Q的坐标；（II）由于等边三角形的内切圆的圆心，也是三角形的重心，故可利用重心坐标公式，求出圆心坐标，从而得到圆的方程．
点评：本题以直线为载体，考查直线的斜率公式，考查圆的方程，属于中档题．
练习册系列答案
黎明文化寒假作业系列答案
相关题目