题目内容
已知O为坐标原点，
=（-1，1），
=（-5，5）集合A={
||
|=2}，
，
∈A且
=λ
（λ∈r，且λ≠0）则
•
=
| OM |
| NM |
| OR |
| RN |
| OP |
| OQ |
| MP |
| MQ |
| MP |
| MQ |
46
46
．分析：根据向量的线性运算，可得点N坐标为（4，-4）且R点的轨迹是以N为圆心，半径为2的圆．进而得到P、Q在圆N上，且M、P、Q三点共线，在Rt△MNS中利用勾股定理，并结合圆的切割线定理即可算出
•
的值．
| MP |
| MQ |
解答：解：∵
=（-1，1），
=（-5，5）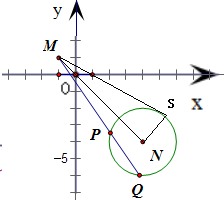
∴向量
=
-
=（4，-4），即点N坐标为（4，-4）
∵集合A={
||
|=2}
∴点R到N的距离等于2（常数），故R点的轨迹是以N为圆心，半径为2的圆
∵
，
∈A且
=λ
（λ∈r，且λ≠0）
∴P、Q在圆N上，且M、P、Q三点共线
设过M的直线与圆N相切于点S，连接NS、NM，则
Rt△MNS中，MN=5
，NS=2，可得MS2=MN2-NS2=50-4=46
由切割线定理，可得
•
=
2=46
故答案为：46
| OM |
| NM |
∴向量
| ON |
| OM |
| NM |
∵集合A={
| OR |
| RN |
∴点R到N的距离等于2（常数），故R点的轨迹是以N为圆心，半径为2的圆
∵
| OP |
| OQ |
| MP |
| MQ |
∴P、Q在圆N上，且M、P、Q三点共线
设过M的直线与圆N相切于点S，连接NS、NM，则
Rt△MNS中，MN=5
| 2 |
由切割线定理，可得
| MP |
| MQ |
| MS |
故答案为：46
点评：本题以向量为载体，求动点的轨迹方程并求数量积
•
的值．着重考查了平面向量的线性运算、平面向量数量积的运算和动点轨迹方程的求法等知识，属于中档题．
| MP |
| MQ |
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目