题目内容
已知函数f(x)= [3ln(x+2)﹣ln(x﹣2)]
[3ln(x+2)﹣ln(x﹣2)]
(I) 求x为何值时,f(x)在[3,7]上取得最大值;
(Ⅱ)设F(x)=aln(x﹣1)﹣f(x),若F(x)是单调递增函数,求a的取值范围.
 [3ln(x+2)﹣ln(x﹣2)]
[3ln(x+2)﹣ln(x﹣2)](I) 求x为何值时,f(x)在[3,7]上取得最大值;
(Ⅱ)设F(x)=aln(x﹣1)﹣f(x),若F(x)是单调递增函数,求a的取值范围.
解:(Ⅰ)f′(x)= [
[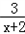 ﹣
﹣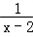 ]=
]=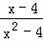
∴当2<x<4时,f′(x)<0,当x>4时,f′(x)>0
∴f(x)在(2,4)上是减函数,在(4,+∞)上是增函数
∴f(x)在[3,7]上的最大值应在端点处取得
f(3)﹣f(7)= [3ln5﹣ln1]﹣
[3ln5﹣ln1]﹣ [ln625﹣ln729]<0,
[ln625﹣ln729]<0,
∴f(3)<f(7)即当x=7时,f(x)取得在[3,7]上的最大值
(Ⅱ)∵F(x)是单调递增函数,
∴F(x)≥0恒成立
又F′(x)=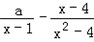 =
=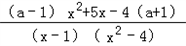
显然在f(x)的定义域(2,+∞)上,(x﹣1)(x2﹣4)>0恒成立.
∴(a﹣1)x2+5x﹣4(a+1)≥0在(2,+∞)上恒成立.
下面分情况讨论(a﹣1)x2+5x﹣4(a+1)>0在(2,+∞)上恒成立时,a的解的情况.
当a﹣1<0时,显然不可能有(a﹣1)x2+5x﹣4(a+1)≥0在(2,+∞)上恒成立.
当a﹣1=0时(a﹣1)x2+5x﹣4(a+1)=5x﹣8>0在(2,+∞)上恒成立.
当a﹣1>0时,又有两种情况:
①52+16(a﹣1)(a+1)≤0;
②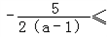 且(a﹣1)﹣22+5×2﹣4(a+1)≥0
且(a﹣1)﹣22+5×2﹣4(a+1)≥0
由①得16a2+9≤0,无解;
由②得a≥﹣ ,a﹣1>0,∴a>1
,a﹣1>0,∴a>1
综上所述各种情况,
当a≥1时(a﹣1)x2+5x﹣4(a+1)≥0在(2,+∞)上恒成立.
∴所求的a的取值范围为[1,+∞).
 [
[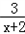 ﹣
﹣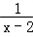 ]=
]=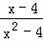
∴当2<x<4时,f′(x)<0,当x>4时,f′(x)>0
∴f(x)在(2,4)上是减函数,在(4,+∞)上是增函数
∴f(x)在[3,7]上的最大值应在端点处取得
f(3)﹣f(7)=
 [3ln5﹣ln1]﹣
[3ln5﹣ln1]﹣ [ln625﹣ln729]<0,
[ln625﹣ln729]<0,∴f(3)<f(7)即当x=7时,f(x)取得在[3,7]上的最大值
(Ⅱ)∵F(x)是单调递增函数,
∴F(x)≥0恒成立
又F′(x)=
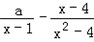 =
=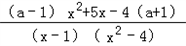
显然在f(x)的定义域(2,+∞)上,(x﹣1)(x2﹣4)>0恒成立.
∴(a﹣1)x2+5x﹣4(a+1)≥0在(2,+∞)上恒成立.
下面分情况讨论(a﹣1)x2+5x﹣4(a+1)>0在(2,+∞)上恒成立时,a的解的情况.
当a﹣1<0时,显然不可能有(a﹣1)x2+5x﹣4(a+1)≥0在(2,+∞)上恒成立.
当a﹣1=0时(a﹣1)x2+5x﹣4(a+1)=5x﹣8>0在(2,+∞)上恒成立.
当a﹣1>0时,又有两种情况:
①52+16(a﹣1)(a+1)≤0;
②
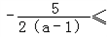 且(a﹣1)﹣22+5×2﹣4(a+1)≥0
且(a﹣1)﹣22+5×2﹣4(a+1)≥0由①得16a2+9≤0,无解;
由②得a≥﹣
 ,a﹣1>0,∴a>1
,a﹣1>0,∴a>1综上所述各种情况,
当a≥1时(a﹣1)x2+5x﹣4(a+1)≥0在(2,+∞)上恒成立.
∴所求的a的取值范围为[1,+∞).

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|