题目内容
已知正项数列{an}的前n项和为 .当n≥2且n∈N*时,点(Sn-1,Sn)在直线
.当n≥2且n∈N*时,点(Sn-1,Sn)在直线 上,数列{bn}满足
上,数列{bn}满足 .
.
(1)求数列{an}的通项公式an;
(2)设数列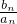 的前n项和为Tn.求Tn.
的前n项和为Tn.求Tn.
解:(1)当n≥2且n∈N*时,点(Sn-1,Sn)在直线 上,
上,
∴2Sn=4Sn-1+1①
∴ ②
②
由②-①得: (2分)
(2分)
由2S2=4S1+1得2(a1+a2)=4a1+1,又 ,
,
∴a2=1,∴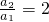 ,(4分)
,(4分)
∴数列{an}是以 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
∴ (6分)
(6分)
(2)∵
∴ (8分)
(8分)
∴
③ ④(10分)
④(10分)
由③-④得: ,
,
∴ .(12分)
.(12分)
分析:(1)由题意可得当n≥22Sn=4Sn-1+1, ,两式相减即可求解
,两式相减即可求解
(2)由(1)可得 ,结合数列的特点,考虑利用错位相减求和即可
,结合数列的特点,考虑利用错位相减求和即可
点评:本题主要考查了数列的递推公式 在数列的通项公式的求解中的应用,及数列求和的错位相减求和方法的应用,要注意该方法适用的范围:若数列{anbn}中,an,bn分别为等差、等比数列
在数列的通项公式的求解中的应用,及数列求和的错位相减求和方法的应用,要注意该方法适用的范围:若数列{anbn}中,an,bn分别为等差、等比数列
 上,
上,∴2Sn=4Sn-1+1①
∴
 ②
②由②-①得:
 (2分)
(2分)由2S2=4S1+1得2(a1+a2)=4a1+1,又
 ,
,∴a2=1,∴
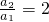 ,(4分)
,(4分)∴数列{an}是以
 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.∴
 (6分)
(6分)(2)∵

∴
 (8分)
(8分)∴

③
 ④(10分)
④(10分)由③-④得:
 ,
,∴
 .(12分)
.(12分)分析:(1)由题意可得当n≥22Sn=4Sn-1+1,
 ,两式相减即可求解
,两式相减即可求解(2)由(1)可得
 ,结合数列的特点,考虑利用错位相减求和即可
,结合数列的特点,考虑利用错位相减求和即可点评:本题主要考查了数列的递推公式
 在数列的通项公式的求解中的应用,及数列求和的错位相减求和方法的应用,要注意该方法适用的范围:若数列{anbn}中,an,bn分别为等差、等比数列
在数列的通项公式的求解中的应用,及数列求和的错位相减求和方法的应用,要注意该方法适用的范围:若数列{anbn}中,an,bn分别为等差、等比数列 
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目